ریاضی هفتم یک نظر بگذارید
ریاضی پایۀ هفتم
دورۀ اوّل متوسطه
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
چگونه ریاضی یاد بگیریم؟
در دورۀ ابتدایی با مفاهیم حساب و هندسه آشنا شدید. در دورۀ اوّل متوسطه از دانش ریاضی خود استفاده می¬کنید و آن را به کار می¬برید تا معلومات ریاضی خود را افزایش دهید؛ اما چگونه باید ریاضیات را آموخت؟
برای یادگیری ریاضی، خودتان دست به کار شوید؛ در کلاس نقش فعّالی داشته باشید؛ فقط شنونده بودن کافی نیست. فعالیت¬های کتاب درسی به شما کمک می¬کنند تا در جریان کلاس سهیم باشید. متن فعالیت¬ها را با دقّت بخوانید و به صورت فردی یا گروهی کارهای خواسته شده را انجام دهید. مهم¬ترین قسمت فعالیت-ها، بخش نتیجه¬گیری است. آن قسمت¬ها را به صورت کامل بنویسید.
فعالیت
نقطۀ A روی محیط دایره حرکت می¬کند. در وضعیت AOB زاویۀ صفر درجه را نشان می¬دهد. وقتی A روی دایره حرکت می¬کند تا برای مثال به نقطۀ B برسد. یک زاویه درست می¬کند. با توجه به جهت¬های + و – نشان داده شده، مشخص کنید هر یک از زاویه¬های زیر چند درجه¬اند؟ با یک عدد علامت¬دار نشان دهید.
کار در کلاس¬ها هم به شما کمک می¬کند تا آموخته¬های خود را به کار برید و هم این فرصت را به معلّم می-دهد تا فرایند آموزش را کامل کند و به سؤال¬های شما پاسخ دهد و اشکالات پیش¬آمده را رفع کند.
کار در کلاس
تساوی¬ها را کامل کنید.
در پایان، تمرین¬ها را در منزل به¬طور کامل انجام دهید. انجام کامل تمرین به این معناست که شما این قسمت را فراگرفته¬اید. اگر نتوانستید به سؤالی جواب دهید، مهمترین کار شما جست¬وجوی راه¬حل از دوستان، هم-کلاسی¬ها یا معلم است. هرگز تمرینی را بدون پاسخ کامل رها نکنید.
تمرین
عددها را با هم مقایسه کنید.
برای انجام کارهای بالا، شما باید توانایی خود را در حل مسئله بالا ببرید. کسی در حل کردن مسئله ماهر شود، می¬تواند فعالیت¬ها را به نتیجه برساند.
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
چگونه مسئله را حل کنیم؟
حل کردن هر مسئله، 4 مرحله دارد. در تمام کتاب وقتی با مسئله¬ای روبه¬رو می¬شوید، این 4 مرحله را در ذهن خود مرور کنید تا کم¬کم در حل کردن مسئله فکر خود را سازمان¬دهی کنید.
مرحلۀ اول؛ غهمیدن مسئله: برای درک مسئله باید آن را خوب بخوانید و درک کنید. کارهای زیر می¬تواند شما را در درک بهتر مسئله کمک کند:
* مسئله را به زبان و کلمات خود بیان کنید. * خواسته¬های مسئله را معلوم کنید.
* مسئله را خلاصه کنید. * شرط¬های خاص مسئله را جدا کنید.
* داده¬ها و اطلاعات مسئله را مشخص کنید. * مسئله را به صورت یک نمایش ساده اجرا کنید.
مرحلۀ دوم؛ انتخاب راهبرد مناسب: در دورۀ ابتدایی با تعدادی از راهبردهای حل مسئله آشنا شدید. دانستن نام و کاربرد هر راهبرد به شما کمک می¬کند تا آن¬ها را مرور و پیدا کنید که کدام یک برای حل مسئله، ممکن است، مفید باشد.
* رسم شکل * حدس و آزمایش
* الگوسازی * زیر مسئله
* حذف حالت¬های نامطلوب * حل مسئله ساده¬تر
* الگویابی * روش¬های نمادین
مرحلۀ سوم؛ حل کردن مسئله: با راهبردی که انتخاب کردید، مسئله را حل کنید. اگر تشخیص دادید که مسئله با آن راهبرد به نتیجه نمی¬رسد، به مرحلۀ دوم برگردید و راهبرد خود را تغییر دهید. گاهی اوقات لازم است به مرحلۀ اوّل برگردید. شاید نکته¬ای در مسئله وجود دارد که شما هنوز به آن توجه نکرده¬اید.
مرحلۀ چهارم؛ بازگشت به عقب: حل کردن مسئله با پیدا شدن پاسخ ریاضی تمام نمی¬شود. ابتدا پاسخ ریاضی خود را در موضوع مسئله تفسیر کنید. آیا پاسخ شما همان خواسته مسئله است؟ آیا جواب شما منطقی است؟ می¬توانید مراحل و عملیات مسئله را بررسی کنید یا مسئله را با راه¬حل دیگری پاسخ دهید.
راهبرد رسم شکل
راهبرد حذف حالت¬های نامطلوب
راهبردالگویابی
راهبرد حدس و آزمایش
راهبرد زیرمسئله
راهبرد حل مسئله ساده¬تر
راهبرد روش¬های نمادین
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
فصل 1
راهبردهای حل مسئله
راهبرد رسم شکل
کشیدن یک شکل مناسب می¬تواند به حلّ مسئله کمک کند یا به طور کامل آن را حل کند؛ به طوری که نیازی به نوشتن عملیات و محاسبه نباشد. گاهی ممکن است شکل را فقط تصور کنید و آن را رسم نکنید. منظور از رسم شکل، نقّاشی نیست؛ بلکه می¬توانید برای این کار شکل¬های ساده بکشید.
1 یک باغچه مستطیل شکل به طول 10 و عرض 5 متر است. اگر به فاصله یک متر از ضلع های باغچه دورتا دور آن را نرده بکشیم، چند متر نرده احتیاج داریم؟
ابتدا یک مستطیل رسم کنید.
دور آن به فاصله یک متر از هر ضلع خط بکشید.
یک مستطیل جدید به وجود می آید. طول و عرض این مستطیل چقدر است؟
2- توپی از ارتفاع 18 متری سطح زمین رها می شود و پس از زمین خوردن، نصف ارتفاع قبلی خود بالا می آید. این توپ از لحظه رها شدن تا سومین مرتبه ای که به زمین می خورد، چند متر حرکت کرده است؟
3- قورباغه¬ای می خواهد از یک دیوار عمودی بالا برود. او با هر جهش 3 متر بالا می رود و هر بار 2 متر سُر می خورد و پایین می آید. اگر ارتفاع دیوار 9 متر باشد، او با چند جهش به بالای دیوار می رسد؟
راهبرد الگوسازی
برای حلّ بعضی از مسئله ها باید همه حالت های ممکن را بنویسید. برای اینکه هیچ حالتی از قلم نیفتد، لازم است آنها را با نظم، الگو و ترتیبی مشخص بنویسید. الگوسازی به شما کمک م یکند تا مطمئن شوید همه حالت ها را نوشته اید. بنابراین در مسئله هایی که لازم است همه جواب ها و پاسخ های ممکن را بنویسید، می توانید از این راهبرد استفاده کنید. با توجّه به نظم و ترتیبی که می سازید، به این راهبرد تفکّر نظام دار نیز می گویند.
1- دو عدد طبیعی پیدا کنید که حاصل ضرب آنها 24 و حاصل جمع آن¬ها کمترین مقدار باشد. جدول را با یک نظم و ترتیب کامل کنید.
کوچک ترین عدد طبیعی چیست؟
حاصل ضرب آن در چه عددی 24 می شود؟
اکنون عدد طبیعی بعدی را در نظر بگیرید و به همین ترتیب عددها را پیدا کنید.
اولین عدد دومین عدد حاصل جمع
1
2 24
12 25
2- با انگشتان یک دست به 5 صورت می توان عدد 1 را نشان داد. به چند صورت می توان عدد 2 را نشان داد؟
3- با رقم های 7، 2 و 5 تمام عددهای سه رقمی ممکن را بنویسید (در عددهای شما می تواند رقم های تکراری هم باشد.)
4- تعداد زیادی سکه های 50 و 100 تومانی داریم. به چند حالت می¬توان کرایه 500 تومانی تاکسی را پرداخت کرد؟
راهبرد حذف حالت¬های نامطلوب
به شرایط و اطّلاعات مسئله توجه کنید و حالت¬های نامطلوب و نادرست را کنار بگذارید؛ آنگاه پاسخ مسئله یا همان حالت¬های مطلوب به دست می¬آیند. برای پیداکردن تمام حالت¬های ممکن می¬توانید از راهبرد الگوسازی استفاده کنید. ابتدا فهرستی از تمام حالت¬ها به دست آورید؛ سپس با توجّه به شرایط گفته شده در مسئله، حالت های نامطلوب را حذف کنید.
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
1- مجموع سنّ سه نفر 14 سال و حاصل ضرب سنّ آن¬ها 70 است. سنّ بزرگ¬ترین نفر چقدر است؟
ابتدا با راهبرد الگوسازی همه حالت¬هایی را که ضرب سه عدد طبیعی برابر 70 می¬شود، بنویسید.
به این جدول چه ستونی باید اضافه کنید تا حالت¬های نامطلوب حذف و فقط حالت مطلوب باقی بماند؟
نفراول نفردوم نفرسوم
2- دوست شما یک عدد حسابی کوچک¬تر از 100 را در نظر گرفت. شما باید با طرح چند سؤال، عدد مورد نظر را پیدا کنید. او فقط می¬تواند به سؤال¬های شما بله و خیر بگوید. چگونه می¬توان عدد مورد نظر را پیدا کرد؟
در واقع از 0 تا 99 ، 100 عدد وجود دارد که فقط یکی مطلوب و مورد نظر است و باقی عددها نامطلوب اند. با این توضیح کدام یک از سؤال های زیر مناسب تر است؟ چرا؟
آیا عدد موردنظر شما 27 است ؟ آیا عدد موردنظر شما زوج است؟
آیا عدد موردنظر شما یک رقمی است ؟ آیا عدد موردنظر شما از 50 بزرگ تراست؟
با توجّه به پاسخی که به سؤال¬های بالا دادید، یک روش طرح سؤال همراه با نظم و ترتیب بیان کنید که بتوان با پرسیدن آن¬ها به عدد موردنظر رسید.
راهبرد الگویابی
در ریاضی با دو نوع الگوی عددی یا هندسی روبه¬رو می شویم. کشف الگو، رابطه و نظم موجود در بین دنباله-های عددی یا هندسی کمک می¬کند تا بتوانید خواسته مسئله را به دست آورید. این راهبرد در مسئله¬هایی کاربرد دارد که بین شکل¬ها یا عددها، الگو و رابطه خاصی وجود داشته باشد.
1- سه عدد بعدی الگوهای زیر را بنویسید. رابطه بین عددها را توضیح دهید.
3- اگر شکل¬ها به همین ترتیب ادامه پیدا کند، چه کسری از شکل شماره 6، رنگی است؟
راهبرد حدس و آزمایش
ممکن است حلّ یک مسئله، روش و راه¬حلّ مستقیمی نداشته باشد یا راه رسیدن به جواب آن طولانی و دشوار باشد. شما می توانید با یک روش منطقی و منظّم پاسخ احتمالی مسئله را حدس بزنید؛ سپس با توجه به شرایط گفته شده در مسئله، حدس خود را بررسی کنید و با توجّه به نتیجه به دست آمده حدس بعدی را بزنید تا کم کم به پاسخ مسئله نزدیک شوید. برای نشان دادن حدس¬ها و آزمایش¬های خود راه¬حل مناسبی پیدا کنید.
1-20 دستگاه دوچرخه و سه چرخه در یک توقفگاه (مصوب فرهنگستان Parking) وجود دارد. اگر تعداد کلّ چرخ¬های آن¬ها 45 عدد باشد، چند دوچرخه و چند سه چرخه در توقفگاه وجود دارد؟
بررسی و آزمایش تعداد سه¬چرخه تعداد دوچرخه
10 10
در حدس اول تعداد دوچرخه¬ها را 10 و تعداد سه¬چرخه¬ها را هم 10 عدد درنظر بگیرید.
با کامل کردن ردیف اول جدول حدس خود را بررسی و آزمایش کنید.
با توجه به نتیجه بررسی، باید تعداد سه¬چرخه¬ها را بیشتر کرد یا دوچرخه¬ها را؟ چرا؟
2- دو زاویه متمم¬اند. یکی از این زاویه¬ها 3 برابر زاویه دیگر است. اندازه هر زاویه را پیدا کنید.
3- به جای چه عددی می¬توان قرار داد؟
به جای عددهای مختلفی را حدس بزنید، از عدد 10 شروع کنید.
راهبرد زیرمسئله
مسئله پیچیده و چند مرحله ای را به چند مسئله ساده تبدیل کنید. فهرستی از این زیرمسئله¬ها را درست کنید؛ سپس به ترتیب به آن¬ها پاسخ دهید. اگر ترتیب زیرمسئله¬ها را درست تشخیص داده باشید، حلّ هر زیرمسئله به حلّ مسئله بعدی کمک می¬کند تا در نهایت به خواسته اصلی مسئله برسید.
1- پس انداز هفتگی محمد، 3000 تومان است. اوحساب کرد 5 هفته پس انداز او، نصف قیمت کیفی است که دوست دارد بخرد. قیمت کیف چقدر است؟
الف) پس انداز 5 هفته چقدر می¬شود؟
ب) اگر این عدد نصف قیمت کیف باشد، قیمت کیف چقدر است؟
2- طول، عرض و عمق یک استخر به ترتیب12 ، 6 و 3 متر است. می¬خواهند کف و دیوارهای این استخر را رنگ کنند. اگر برای هر متر مربع 3/0 کیلوگرم رنگ لازم باشد، برای رنگ کردن استخر چند کیلوگرم رنگ نیاز است؟
3- میوه فروشی، امروز 40 کیلوگرم سیب به قیمت هرکیلوگرم 2500 تومان و 80 کیلوگرم پرتقال به قیمت هرکیلوگرم 1500تومان خرید. او هر کیلوگرم سیب را 3000 تومان و هر کیلوگرم پرتقال را 2000 تومان فروخت. این میوه فروش، از این کار خود چقدر سود برده است؟
راهبرد حل مسئلۀ ساده تر
برای حلّ بعضی از مسئله ها،ابتدا مسئله ای ساده تر را که با مسئله اصلی در ارتباط است، حل می کنیم. سپس
با استفاده از نتیجه و پاسخ مسئله ساده شده، جواب مسئله اصلی را به دست می¬آوریم. برای ساده کردن مسئله می¬توان از عددهای تقریبی یا عددهای کوچک¬تر استفاده کرد. برای نتیجه¬گیری و پیدا کردن پاسخ مسئله اصلی از راهبرد الگویابی استفاده می¬کنیم و الگوی کشف شده در مسئله ساده را به مسئله اصلی مرتبط می¬کنیم.
1- قطر خورشید 1392530 کیلومتر و قطر کره زمین 6/12756 کیلومتر است. قطر خورشید تقریباً چند برابر قطر زمین است؟
برای ساده شدن مسئله بهتر است از عددهای تقریبی استفاده کنید.
خلاصه مسئله ساده شده را بنویسید و پاسخ دهید.
2 حاصل عبارت مقابل را به دست آورید .
به جای حل کردن عبارت بالا، ابتدا ساده شده این مسئله را حل کنید.
در پاسخ¬ها چه الگو و رابطه¬ای تشخیص می¬دهید که به کمک آن بتوانید پاسخ مسئله اصلی را بدون محاسبه بنویسید؟
3- اگر 10 نقطه را که هیچ سه¬تای آنها روی یک خط نیستند، دو به دو به هم وصل کنیم؛ چند پاره خط به وجود می آید؟
تعداد پاره خط¬ها در واقع مجموع تعداد ضلع¬ها و تعداد قطرهاست.
یک الگو پیدا کنید و برای 10 نقطه نتیجه¬گیری کنید.
راهبرد روش های نمادین
بسیاری از مسئله¬ها را می¬توانیم به کمک نمادهای جبری به یک معادله تبدیل کنیم. از فصل سوم به بعد می-توانید از این راهبرد نیز برای حلّ مسئله استفاده کنید. در بعضی از مسئله¬ها هم می¬توانیم از مدل¬سازی هندسی استفاده کنیم. تبدیل مسئله به یک شکل هندسی و حلّ هندسی آن نیز نوعی روش نمادین یا مدل-سازی به شمار می¬رود.
1- احمد 30000 تومان پول داشت. او 4 دفتر خرید و 2000 تومان برایش باقی ماند. قیمت هر دفتر چقدر است؟
متن این سؤال را می¬توانید با تساوی مقابل نشان دهید.
مربع نشان دهنده چه چیزی است؟
اکنون می¬توانید عددی را که باید در مربع قرار گیرد، حدس بزنید و آزمایش کنید.
(در فصل سوم، این مسئله را به روش دیگر حل خواهید کرد.)
2- فاطمه کتاب داستانی را در 6 ساعت مطالعه کرد و 10 صفحه از آن باقی ماند. اگر این کتاب 100 صفحه داشته باشد، فاطمه به طور متوسط در هر ساعت چند صفحه از آن را مطالعه کرده است؟
3- یک سالن مستطیل شکل است. می¬خواهند در مکانی از سقف این سالن دریچه خنک کن (مصوب فرهنگستان Cooler) قرار دهند؛ به طوری که از 4 گوشه آن به یک اندازه باشد. محل دریچه را تعیین کنید.
مرور راهبردها
در حل این مسئله¬ها از راهبردهایی که آموخته¬اید، استفاده کنید. ممکن است در حلّ مسئله¬ای راه جدیدی به ذهن شما برسد که با راهبردهای آموزش داده شده متفاوت باشد. برای حلّ مسئله¬ها می¬توانید از ماشین حساب استفاده کنید. درباره راهبردهای مختلف با هم کلاسی¬های خود گفت¬وگو کنید. ممکن است یک مسئله با چند راهبرد حل شود، یا چند نفر از یک راهبرد استفاده کنند؛ ولی شیوه به کار بردن آن¬ها متفاوت باشد. برای مثال چند نفر یک مسئله را با راهبرد رسم شکل حل می¬کنند؛ اما ممکن است نحوه شکل کشیدن آن¬ها متفاوت باشد. در یک کلاس ریاضی خوب و فعّال، تنوّع راهبرد و راه¬حل وجود دارد.
1- 1/3 دانش¬آموزان کلاسی بسکتبال و 1/5 دانش¬آموزان آن کلاس فوتبال بازی می¬کنند. سایر دانش-آموزان که تعدادشان 14 نفر است، آن¬ها را تماشا می¬کنند. این کلاس چند دانش¬آموزان دارد؟
2- مساحت مربعی به ضلع 100 سانتی متر، 1متر مربع است. اگر از ضلع مربع 10 درصد کم کنیم، مساحت مربع چند درصد کم می¬شود؟
3 کشاورزی زمین خود را به نسبت های زیر بذر پاشی کرده است:
گندم % 45 : جو: 5/37% ذرت: 5/17%
اگر مساحت زمین او 15 هکتار باشد، مساحت زیر کشت هر بذر را حساب کنید.
4- حاصل عبارت رو به رو را پیدا کنید .
5- در یک کارگاه تولید کفش، 4960 جفت کفش تولید شده است. 3/8 آن¬ها پسرانه و بقیه دخترانه است. اگر قیمت هر جفت کفش پسرانه 27000 تومان و قیمت هر جفت کفش دخترانه 34000 تومان باشد، درآمد این کارگاه چقدر است؟
6- سارا یک بازی روی صفحۀ شطرنجی انجام می¬دهد. مهرۀ او روی خانۀ [2/3] است. او ابتدا مهره¬اش را 3 خانه به سمت راست، سپس 4 خانه به سمت بالا و در انتها 2 خانه به سمت چپ آورد. در حال حاضر مهرۀ سارا روی کدام خانه قرار دارد؟
7- چه کسری از شکل زیر رنگی است؟ توضیح دهید.
8- اگر دیوارهای یک استخر با طرح زیر کاشی¬کاری شده باشد، چه کسری از دیوار کاشی آبی دارد؟
9- به چند حالت حاصل ضرب 2 عدد طبیعی 36 می¬شود؟ در کدام حالت حاصل جمع، کمترین مقدار است؟
10- عددی را 5 برابر و 3 واحد از آن کم کردیم، حاصل 32 شد. عدد مورد نظر چند است؟
در این قسمت برای خود فهرستی از راهبردهای حلّ مسئله تهیه کنید تا در هنگام حل فعّالیت¬ها و مسئله¬های کتاب از آن استفاده کنید. هنگام حل مسئله می¬توانید از ماشین حساب نیز استفاده کنید.
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
فصل 2
عددهای صحیح
از عددهای صحیح (علامت¬دار) می¬توان برای بیان وضعیت سرما و گرمای هوا؛ همچنین عمق و ارتفاع نسبت به سطح زمین یا سطح دریا استفاده کرد.
معرفی عددهای علامت¬دار
جمع و تفریق عددهای صحیح (1)
جمع و تفریق عددهای صحیح (2)
ضرب و تقسیم عددهای صحیح
معرفی عددهای علامت¬دار
1- متحرکی از نقطه A روی محیط دایره حرکت می¬کند تا به نقطه B برسد و زاویه AOB را بسازد. وقتی متحرک روی نقطه A است اندازه زاویه صفر است. اندازه هر یک از زاویه¬های زیر را با توجه به جهت¬های مثبت و منفی مشخص شده با یک عدد علامت دار نشان دهید.
2- در سال گذشته با نمایش عددهای صحیح روی محور آشنا شدید و آموختید که قرینه هر عدد منفی عددی مثبت و قرینه هر عدد مثبت عددی منفی است. قرینه صفر هم خود صفر است. برای نمایش قرینه هر عدد از نماد (-) در سمت چپ آن عدد استفاده می¬کنیم. با کمک محور، مانند نمونه تساوی¬ها را کامل کنید.
3- مانند نمونه و به کمک محور بالا تساوی¬ها را کامل کنید.
از تساوی¬های بالا چه نتیجه¬ای می¬گیرید؟
عددهای صحیح مثبت همان عددهای طبیعی¬اند، برای مثال می¬توان نوشت:
+3=3 و 7=+7
عددهای صحیح شامل عددهای صحیح مثبت، صفر و عددهای صحیح منفی می¬شوند.
کار در کلاس
تساوی را کامل کنید.
فعالیت
1- مانند نمونه¬ها برای هر حرکت روی محور یک عدد صحیح (مثبت، منفی یا صفر) بنویسید.
2- وقتی دو حرکت پشت سرهم انجام می¬شود، می¬توانیم یک جمع بنویسیم. مانند نمونه برای هر حرکت یک جمع بنویسید.
3- عبارت (2+)- (4+) را می¬توانید به¬صورت تفریقی که در دورۀ ابتدایی می¬نوشتید، تبدیل کنید؛ یعنی: (+4)-(+2)=4-1 تفریق را هم می¬توانیم به¬صورت جمع بنویسیم؛ مانند: 4-2=4+(-2)
مانند نمونه¬ها تساوی¬ها را کامل کنید.
کار در کلاس
ابتدا تفریق¬ها را به جمع تبدیل کنید سپس در دفتر خود برای هر جمع یک محور رسم کنید و به کمک آن حاصل را به دست آورد.
1- جمع و تفریق¬ها را روی محور نشان دهید و حاصل را به دست آورید. ابتدا تفریق¬ها را به صورت جمع بنویسید.
از این فعالیت چه نتیجه¬ای می¬گیرید؟
2- جمع و تفریق¬ها را روی محور نشان دهید و حاصل را به دست آورید. ابتدا تفریق را به صورت جمع بنویسید.
از این فعالیت چه نتیجه¬ای می¬گیرید؟
تمرین
1- عددها را با هم مقایسه کنید.
2- مانند نمونه، گستردۀ عددها را بنویسید و به جمع تبدیل کنید.
3- عدد قبل و بعد هر یک از عددها را بنویسید.
4- عددها را به طور تقریبی روی محور نشان دهید.
جمع و تفریق عددهای صحیح (1)
فعالیت
1- اگر هر دایرۀ سفید () نشان دهندۀ 1+ و هر دایرۀ سیاه () نشان دهندۀ 1- باشد، وقتی مانند شکل زیر آن¬ها را روی هم و داخل یک ظرف می¬ریزیم (به عبارت دیگر با هم جمع می¬کنیم)، حاصل آن چقدر می-شود؟ چرا؟
2- با توجه به تعریف دایره¬های سیاه و سفید مشخص کنید هر شکل چه عددی را نشان می¬دهد؟
برای شکل سوم یک عبارت جمع بنویسید. ـــــــــــ = ــــــــــــ + ـــــــــــ
3- مانند نمونه حاصل جمع و تفریق¬ها را با این روش پیدا کنید. فراموش نکنید که ابتدا باید تفریق را به جمع تبدیل کنید.
4- علاوه بر این روش، پیدا کردن حاصل جمع و تفریق با محور را نیز آموخته¬اید.
اکنون با یکی از این دو روش، حاصل را به دست آورید. مانند نمونه برای هرکدام نتیجه را بنویسید.
نتیجه: اگر هر دو عدد مثبت باشند، حاصل جمع آن¬ها مثل جمع دو عدد طبیعی است.
نتیجه: اگر هردو عدد منفی باشند، ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
کار در کلاس
کار در کلاس
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
حاصل جمع و تفریق ها را به دست آورید.
فعالیت
در هر قسمت حاصل جمع و تفریق ها را به هر روشی که می¬شناسید، به دست آورید و نتیجه را بنویسید.
نتیجه: اگر در جمع دو عدد صحیح یکی از دو عدد مثبت و دیگری منفی باشد و بدون در نظر گرفتن علامت¬ها مقدار مثبت بیشتر باشد، ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
نتیجه: اگر در جمع دو عدد یکی از دو عدد مثبت و دیگری منفی باشد و بدون در نظر گرفتن علامت¬ها مقدار عدد منفی بیشتر باشد ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
کار در کلاس
با توجه به نتایج بالا حاصل عبارت¬ها را به دست آورید.
تمرین
1- عددها را از کوچک¬تر به بزرگ¬تر و از چپ به راست مرتب کنید.
23- و 12 و -34 و -5 و 0 و 45 و 15- و 5 و 1- و 2
پاسخ مسئله های زیر را در دفترتان بنویسید.
2- طبقه همکف یک ساختمان را با صفر و طبقه¬های بالای همکف را با عددهای مثبت و طبقه¬های زیر همکف را با عددهای منفی نشان می¬دهیم. حال مسئله زیر را حل کنید.
شخصی در طبقه 5+ سوار آسان بر (مصوب فرهنگستانelevator, ascenseur ) شد. او ابتدا 3 طبقه بالا رفت و پس از انجام کاری 6 طبقه به پایین آمد و دوباره برای خرید چای 2 طبقه پایین رفت و در همان طبقه هزینه¬های خرید خود را حساب کرد. سپس دوباره 2 طبقه پایین رفت و در توقفگاه (مصوب فرهنگستان Parking ) سوار ماشین خود شد. ماشین این شخص در کدام طبقه بود؟
3- دمای هوای شهرکرد 2 درجه زیر صفر است. اردبیل 8 درجه از شهرکرد سردتر است. دمای هوای شهر اردبیل چند درجه است؟
4- دمای شهرکرمان، سنندج و یاسوج به ترتیب ١١ درجه بالای صفر، 6 درجه زیر صفر و 10 درجه زیر صفر است. سنندج چند درجه از کرمان سردتر است؟ یاسوج چند درجه از سنندج سرد تر است؟
5- در جای خالی عدد مناسب بنویسید.
6- در مثلث مقابل، عدد روی هر ضلع، از مجموع عددهای دو رأس به دست می¬آید.
جاهای خالی را کامل کنید.
7- حاصل عبارت¬ها را به دست آورید.
جمع و تفریق عددهای صحیح (2)
فعالیت
1- مانند نمونه جمع و تفریق دو عدد دو رقمی را به جمع و تفریق عددهای یک رقمی تبدیل کنید. سپس با توجه به جدول حاصل را به یک جمع تبدیل کنید.
به همین ترتیب می¬توانید جمع و تفریق چند عدد دو رقمی را انجام دهید.
٢ حاصل عبارت¬های ردیف اول را به کمک ٤ قانونی که در درس قبل نتیجه گرفتید، نیز پیدا کنید. روش کار را توضیح دهید.
کار در کلاس
حاصل عبارت¬ها را مانند نمونه بالا انجام دهید.
فعالیت
1- در این نمونه به کمک محور و به صورت تقریبی محل جواب و علامت آن تعیین می شود و از روی حرکت پیکانه (مصوب فرهنگستانarrow , fleche ) می¬توان روش محاسبه را حدس زد. با توجه به شکل، حاصل مثبت و جواب 70-58=12 است.
اکنون حاصل عبارت¬های زیر را به دست آورید. برای هر کدام یک محور و حرکت تقریبی رسم کنید.
2- حاصل هر عبارت را به کمک ماشین حساب به دست آورید و درستی پاسخ¬های خود را بررسی کنید. برای منفی کردن عددها از کلید استفاده کنید. این کلید عدد روی صفحه را قرینه می¬کند. برای وارد کردن عدد ٤٣ -دکمه¬ها را به ترتیب از چپ به راست وارد کنید. برای رسیدن به 43- چه راه¬حل دیگری دارید؟
کار در کلاس
1- بدون محاسبه کردن فقط تعیین کنید که حاصل عبارت مثبت است یا منفی .
2- حاصل عبارت¬ها را مانند نمونه به صورت تقریبی به دست آورید.
3- حاصل دقیق عبارت¬های بالا را با ماشین حساب به دست آورید و با پاسخ خود مقایسه کنید.
تمرین
1- حاصل عبارت¬های زیر را به دست آورید.
2- یک زیر دریایی 450 متر پایین تر از سطح دریا قرار دارد. زیر دریایی دیگری150 متر از آن بالاتر است. موقعیت زیر دریایی دوم نسبت به سطح دریا را با یک عدد علامت¬دار نشان دهید.
3- از هر روشی که می¬خواهید حاصل را به دست آورید.
4- ساختمانی از 7 طبقه روی همکف و 3 طبقه زیر همکف تشکیل شده است. احمد در طبقه 2- است. او ابتدا 3 طبقه بالا رفت؛ بعد 2 طبقه پایین آمد و از آنجا 5 طبقه بالا رفت. احمد هم اکنون در کدام طبقه است؟
5- نقاط مشخص شده به طور تقریبی چه عددی را نشان می¬دهند؟
6- حاصل عبارت¬های زیر را به صورت تقریبی به دست آورید.
حاصل هر عبارت بالا را با ماشین حساب به دست آورید و با پاسخ خود مقایسه کنید.
7- جاهای خالی را کامل کنید.
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
ضرب و تقسیم عددهای صحیح
فعالیت
1- به کمک محور و حرکت انجام شده روی آن یک عبارت جمع و یک عبارت ضرب بنویسید و حاصل را به دست آورید.
2- به الگوهای عددی زیر توجّه کنید. پس از اینکه رابطه بین عددها را پیدا کردید، جملات زیر هر کدام را کامل کنید، سپس بقیه هر الگو را کامل کنید.
حاصل¬ضرب¬ها …………. کم می¬شوند. حاصل ضرب¬ها ………….. اضافه می-شوند.
با توجّه به الگویی که کشف کرده¬اید، جدول ضرب مقابل را کامل کنید.
کار در کلاس
با توجّه به فعالیت بالا جدول مقابل را کامل کنید.
به کمک آن حاصل ضرب ها را بنویسید.
فعالیت
1- در دوره دبستان برای نشان دادن ضرب و تقسیم عددها، از شکلی مانند نمونه زیر استفاده می¬کردید.
ضرب¬های زیر را ابتدا با محور نشان دهید. سپس تقسیم¬های متناظرشان را بنویسید.
بدون استفاده از محور برای هر یک از ضرب¬های فوق تقسیم دیگری بنویسید.
2- با توجه به تقسیم¬های بالا جدول زیر را برای تقسیم دو عدد کامل کنید و حاصل تقسیم¬ها را به دست آورید.
کار در کلاس
1- حاصل عبارت¬ها را به دست آورید.
2- حاصل ضرب عددهای روی رأس¬های مثلث، روی هر ضلع نوشته شده است.
جاهای خالی را کامل کنید.
3- الگوهای عددی را کامل کنید.
تمرین
1- جملات زیر را کامل کنید.
* اگر حاصل ضرب یک عدد طبیعی در یک عدد صحیح، منفی شود، آن عدد صحیح ـــــــــ است.
* اگر حاصل تقسیم دو عدد صحیح بر هم عددی منفی شود، یکی از آن عددهای صحیح ـــــــــ و دیگری ــــــــ است.
* اگر ضرب دو عدد صحیح صفر شود، حداقل یکی از آن¬ها ـــــــــ است.
* اگر حاصل تقسیم دو عدد صحیح مثبت باشد، ضرب آن دو عدد صحیح ــــــــــ است.
2- بدون محاسبه مشخص کنید که حاصل عبارت مثبت یا منفی است.
3- در جاهای خالی عدد مناسب بنویسید.
4- همه عددهای صحیح ممکن که می¬توانند به جای و قرار بگیرند را بنویسید. -12= ×
5- حاصل عبارت¬های زیر را به دست آورید.
6- قطاری از مشهد به سوی تهران در حرکت است. طول مسیر 1200 کیلومتر است و قطار در هر ساعت60 کیلومتر حرکت می کند. شهر شاهرود را که در نیمه راه است، مبدأ مقایسه در نظر بگیرید. زمان رسیدن به شاهرود را صفر و قبل از آن را منفی و بعد از آن را مثبت در نظر بگیرید و به سؤال¬های زیر پاسخ دهید:
قطارچه ساعتی از مشهد حرکت کرده است؟
چه ساعتی به تهران می¬رسد؟
قطار در ساعت 3- در چه فاصله ای از شاهرود بوده است؟
در چه ساعتی 240 کیلومتر بعد از شاهرود است؟
جدول زیر را کامل کنید.
مرور فصل 2
مفاهم و مهارت¬ها
در این فصل واژه¬های زیر به کار رفته¬اند. مطمئن شوید که می¬توانید با جملات خود آن¬ها را تعریف کنید. برای هر کدام یک مثال بزنید.
* عدد علامت¬دار * عدد صحیح * قرینۀ عدد * گستردۀ عدد صحیح
در این فصل روش¬های اصلی زیر مطرح شده¬اند. با یک مثال هرکدام را توضیح دهید و در دفتر خود یک خلاصۀ درس تهیه کنید.
قراردادی برای جهت¬های مثبت و منفی
محور عددهای صحیح و مرتب کردن عددهای صحیح (مثبت – صفر – منفی)
قرینۀ قرینۀ یک عدد صحیح هر عدد صحیح مثبت، عددی طبیعی است.
تبدیل تفریق به جمع جمع و تفریق روی محور
جمع و تفریق با دایره¬های سیاه و سفید مقایسه و مرتب کردن عددهای صحیح
جمع و تفریق دو عدد صحیح تعیین علامت در ضرب و تقسیم
ضرب و تقسیم دو عدد صحیح انجام عملیات عددهای صحیح به صورت ذهنی
انجام عملیات عددهای صحیح به صورت تقریبی و با ماشین حساب
حل مسائل مربوط به عددهای صحیح
کاربرد
کاربرد این درس را در فصل¬های بعد نیز خواهید دید. در فصل عبارت جبری، ساده کردن عبارت¬های جبری به محاسبۀ عددهای صحیح تبدیل می¬شود.
این درس در زندگی روزمره برای نشان دادن عددهای علامت دار مثل درجه هوا، ارتفاع نسبت به سطح دریا و… کاربرد دارد. شما می توانید کاربردهای دیگری برای آن پیدا کنید؟
تمرین¬های ترکیبی
درصورتی که تمرین¬های ترکیبی زیر را بتوانید انجام دهید، مطمئن می¬شوید، این فصل را به خوبی آموخته-اید.
1- حاصل عبارت¬های زیر را به دست آورید.
2- دمای هوا در تبریز دو درجه زیر صفر و دمای اردبیل 3 برابر آن است. میانگین دمای این دو شهر چند درجه است؟
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
فصل 3
جبر و معادله
تبدیل مسائل زندگی روزمره به عبارت¬ها و معادله¬های ریاضی را مدل¬سازی می¬گویند. برای مثال هزینه کرایه یک اتوبوس عبارت است از یک قیمت ثابت برای 3 ساعت اول و یک قیمت برای هر ساعت اضافه بعد از 3 ساعت؛ بنابراین می¬توان هزینه اتوبوس را به صورت یک عبارت جبری به صورت C = a+nbنمایش داد. حروف b، a، C و n به چه معنی هستند؟
الگوهای عددی
عبارت¬های جبری
مقدار عددی یک عبارت جبری
معادله
الگوهای عددی
فعالیت
1- یک تشک کشتی به شکل مربّع است. جدول زیر را کامل کنید.
2- اکنون با توجّه به شکل¬های زیر و الگویی که مشاهده می¬کنید، ابتدا شکل پنجم و ششم را رسم و سپس جدول را کامل کنید.
3- شکل¬های زیر با چوب کبریت درست شده¬اند و به همین ترتیب ادامه پیدا می¬کنند. با توجّه به آن¬ها جدول را کامل کنید. ابتدا شکل¬های چهارم و پنجم را رسم کنید.
با توجّه به الگویی که در جدول مشاهده می¬کنید، توضیح دهید چه رابطه¬ای بین شماره شکل و تعداد چوب کبریت¬ها وجود دارد؟ بنویسید. n ام چند چوب کبریت خواهد داشت؟ تعداد چوب کبریت¬ها را بر حسب n شکل
حال با توجّه به رابطه¬ای که به دست آوردید، تعداد چوب کبریت¬های شکل بیستم را پیدا کنید.
در فعالیت بالا، محیط یک مربع به ضلع a، برابر با 4×a=4a است. حرف a یک متغیر نامیده می¬شود. در جبر، متغیرها، نمادهایی برای بیان عددهای نامعلوم یا مقادیر غیرمشخص¬اند.
کار در کلاس
1- در دبستان با محیط و مساحت دایره آشنا شده¬اید. محیط و مساحت دایره را با استفاده از متغیّرها نشان دهید.
2- نمودار مقابل چه کاری انجام می¬دهد؟
توضیح دهید: ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
نمودارها را کامل کنید.
3- این نمودارها چه کاری انجام می¬دهند؟
توضیح دهید: ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
نمودارها را کامل کنید.
4- جملۀ nام الگوهای عددی را مانند نمونه بنویسید. ابتدا سه عدد بعدی هر الگو را بنویسید.
فعالیت
به کمک حروف و نوشتن عبارت¬های جبری قوانینی را که تاکنون در ریاضی آموخته¬اید و با عبارت کلامی بیان می¬کردید، می¬توانید است. حالا معنای هر تساوی a + b = b + a به صورت جبری بنویسید. برای مثال می¬دانیم عمل جمع خاصیت جابه¬جایی دارد، یعنی را بیان کنید.
تمرین
1- در مثلث متساوی¬الساقین مقابل، اندازۀ ساق را با a و قاعده را با b نشان می¬دهیم.
الف) چرا هر دو ساق را با a نشان می¬دهیم؟
ب) محیط مثلث را به دست آورید.
ج) مساحت مستطیل را با عبارت جبری بنویسید.
ــــــــــ + ـــــــــــ + ـــــــــــــ = P= محیط
2- هزینه چاپ کارت ویزیت به این شرح حساب می¬شود: 300 تومان قیمت پایه و 10 تومان برای هر کارت. هزینه چاپ چقدر می¬شود؟
3- صفحاتی باشد که حمید در یک روز می خواند، n حمید هر روز چند صفحه قرآن می¬خواند. اگر تعداد صفحاتی را که او در یک هفته می¬خواند، با یک عبارت جبری نشان دهید.
4- هزینۀ ورودی یک اردوگاه برای هر مدرسه 000/200 تومان و برای هر نفر 1000 تومان است. هزینۀ این اردوگاه را برای مدرسه¬ای که تعداد دانش¬آموزانش a است، با یک عبارت جبری بنویسید.
5- جملۀ nام الگوهای زیر را بنویسید.
6- شکل nام چند چوب کبریت خواهد داشت؟
7- اگر عدد x وارد نمودارهای زیر شود، چه عددی خارج می¬شود؟ تفاوت این دو نمودار را توضیح دهید.
عبارت¬های جبری
فعالیت
1- محیط مربّع مقابل را به دست آورید. ــــــــــ + ــــــــــ + ــــــــــ + ـــــــــــ = P
a+a+a+a=4a
2- محیط مثلث متساوی¬الاضلاع را به دو صورت به دست آورید.
3- حالا محیط مثلث متساوی¬الساقین و مستطیل را به دست آورید.
آیا می¬توانیم a را با a جمع کنیم؟ چرا؟ ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
آیا می¬توانیم a را با b جمع کنیم و با یک جمله نشان دهیم؟ چرا؟ ــــــــــــــــــــــــــــــــــــــــ
یک عبارت جبری، شامل یک یا چند عدد، متغیّر و عمل¬هایی مثل جمع، تفریق، ضرب و تقسیم است. در زیر نمونه¬هایی از عبارت¬های جبری آورده شده است:
ز می شود؛ «×» یا پرانتز برای حاصل ضرب بین آن¬ها استفاده می¬شود و از نماد «.» در یک عبارت جبری، اغلب از علامت را y و x به عنوان یک متغیّر اشتباه شود. در زیر حاصل ضرب دو متغیر«x» زیرا ممکن است علامت ضرب با نماد انگلیسی به صورت¬های مختلف نمایش داده¬ایم که همگی آن¬ها، یکسان¬اند و هیچ فرقی با یکدیگر ندارند:
فعالیت
1- در بعضی از کشورها میوه را به صورت دانه¬ای می¬فروشند. اگر قیمت هر سیب را با a و قیمت هر گلابی را با b نشان می¬دهیم، موارد زیر را با عبارت جبری نشان دهید.
قیمت 5 سیب: قیمت 7 گلاب: قیمت 3 سیب و 2 گلابی:
اگر فردی از میوه فروشی در یک روز 3 سیب خریده باشد و در روز بعد 2 سیب و 4 گلابی خریده باشد، مجموع هزینه این دو خرید چقدر می¬شود؟
2- الف) مساحت هر دو مستطیل را با عبارت جبری نشان دهید.
ب) دو مستطیل را کنار هم گذاشته¬ایم. توضیح دهید مساحت این شکل چگونه به دست آمده است؟
ج) پاسخ¬های الف و ب را با هم مقایسه کنید.
3- مانند سؤال 2برای شکل زیر یک تساوی بنویسید.
توضیح دهید که با کمک تساوی بالا چگونه می¬توان یک عدد بیرون پرانتز را در جمله¬های آن ضرب کرد.
هر کدام از عبارت 2، a، 3a، 8b و 5b یک جمله است. دو جملۀ a، 3a متشابه¬اند: اما 8b و 3a متشابه نیستند. برای ساده کردن عبارت¬های جبری، فقط جمله¬های متشابه را با هم در نظر می¬گیریم و آن¬ها را با هم جمع یا تفریق می¬کنیم. گفتنی است که در ساده کردن یک عبارت جبری، استفاده از قوانین مربوط به اعمال که در درس¬های گذشته خوانده¬اید، مانند ضرب عددهای منفی در مثبت، منفی در منفی، مثبت در مثبت باید رعایت شود. خاصیت جابه¬جایی اعمال جمع و ضرب، خاصیت شرکت¬پذیری ضرب و بی¬اثر بودن پرانتز در ضرب، (ab)c، a(bc) از اهمیت زیادی برخوردار است.
کار در کلاس
حاصل عبارت¬های جبری زیر را به ساده¬ترین صورت ممکن بنویسید.
در زیر شیوه جمع کردن جملات متشابه در عبارت جبری مشخص شده است.
همچنین نحوه ضرب کردن یک عدد در پرانتز مشخص شده است.
توضیح دهید که چگونه از روی عددهای صحیح که در فصل دوم آموختید، برای ساده کردن عبارت¬های جبری استفاده می¬کنید.
تمرین
1- عبارت های کلامی زیر را به عبارت جبری تبدیل کنید.
الف) هشت واحد بیشتر از یک عدد ب) هفت تا کمتر از 4 برابر یک عدد
ج) نه تا بیشتر از حاصل تقسیم یک عدد بر 5 د) دو سوم محیط (P)
2- فاطمه قصد دارد با جمع کردن پول خود یک چادر ملی که توسط بنیاد ملی مد و لباس اسلامی – ایرانی هزینه معرفی شده است، خریداری کند. قیمت این چادر 5d+s است که در آن d قیمت یک کمتر چادر و s هزینۀ دوخت چادر است. اگر چادر را متری 10000 تومان خریده باشد و هزینۀ دوخت آن 20000 تومان باشد، پول چادر فاصله چقدر می¬شود؟
3- عبارت¬های جبری زیر را به صورت کلامی توضیح دهید.
4- محیط و مساحت شکل¬ها را به صورت جبری بنویسید.
5- عبارت¬های جبری را ساده کنید.
6- کدام عبارت جبری زیر را می¬توان به صورت ساده¬تری نوشت؟ چرا؟
مقدار عددی یک عبارت جبری
فعالیت
1- به شیوه شمارش تعداد دایره¬ها توجه کنید. چه رابطه¬ای بین آن و شماره شکل¬ها وجود دارد؟
الف) تعداد دایره¬های شکل 4 و شکل nام را بنویسید.
ب) با کمک عبارتی که برای جمله nام نوشته¬اید، تعداد دایره¬های شکل دهم را پیدا کنید.
2- اگر جملۀ nام یک الگو 3n-5 باشد، جملۀ چهارم و دهم را پیدا کنید.
3- عبارت 2n-7 را به ازای عددهای داده شده پیدا کنید. مانند نمونه راه¬حل را بنویسید.
4- برای پیدا کردن محیط تشک رابطۀ P=4a را نوشته¬اید. محیط یک تشک کشتی به طول 5 متر را پیدا کنید.
5- در نمودار جبری زیر به جای x مقدار 3 را قرار دهید و حاصل را پیدا کنید. عبارت¬های جبری نمودار را کامل کنید.
در یک عبارت جبری اگر به جای متغیّر یا متغیّرهای آن، عدد یا عددهای معیّنی قرار دهیم، مقدار عددی آن عبارت به دست می¬آید. در انجام عملیات محاسبۀ مقدار عبارت، ترتیب انجام عملیات را که سال گذشته آموخته¬اید، رعایت کنید. در مثال زیر به نحوۀ ساختن یک عبارت عددی و سپس محاسبه و رعایت ترتیب انجام عملیات توجه کنید.
کار در کلاس
1- حسن و حسین مقدار عددی جبری زیر را به ازای s=3، t=6 محاسبه کرده¬اند. کدام یک پاسخ را دست به دست آورده است؟ دلیل خود را بنویسید.
2- مقدار عددی عبارت را به ازای a=2 به دست آورید.
3- مستطیل مقابل را درنظر بگیرید.
الف) یک عبارت جبری برای پیدا کردن مساحت آن بنویسید.
ب) اگر n=4 باشد، مساحت مستطیل را پیدا کنید.
4- مقدار عددی عبارت زیر را به ازای x=3 و y=3 به دست آورید.
فعالیت
مقدار عددی عبارت جبری را به ازای x=2 و y=3 پیدا کنید.
اکنون ابتدا عبارت جبری را ساده کنید؛ سپس مقدار آن را به ازای عددهای داده شده، پیدا کنید.
از مقایسه جواب¬ها چه نتیجه¬ای می¬گیرید؟
تمرین
1- سارا از یک فروشگاه کتاب تعداد k جلد کتاب نو به مبلغ هر کدام 7000 تومان و s جلد کتاب دست دوم به مبلغ هر کدام 2000 تومان خریده است.
الف) یک عبارت جبری برای مجموع خرید سارا بنویسید .
ب) اگر سارا 3 تا کتاب نو و 6 کتاب دسته دوم خریده باشد، او در مجموع چه مبلغی پرداخت کرده است؟
2- کتابخانه ملی یکی از مراکز معتبر در ایران است که کتاب¬های خطّی و چاپی دانشمندان ایرانی در دوران باشکوه ایرانی در دوران باشکوه تمدن اسلامی (مخصوصاً کتاب¬های قرن¬های دوم تا هفتم هجری) را نگهداری می¬کند. اگر m نسخۀ خطی و n و نسخۀ چاپی در این کتابخانه نگهداری شود و از هر نسخۀ خطی 2 ریزفیلم (مصوب فرهنگستان microfilm) و از هر نسخۀ چاپی یک ریزفیلم تهیه شده باشد، تعداد کل ریزفیلم¬ها را با یک عبارت جبری نشان دهید.
اگر 1000 نسخه خطی و 5000 نسخه چاپی وجود داشته باشد، تعداد کلّ ریزفیلم¬ها را پیدا کنید.
3- مقدار عددی عبارت¬های جبری را به ازای عددهای داده شده به دست آورید.
4- مدیر یک دبیرستان قصد دارد دانش¬آموزان پایه هفتم را برای بازدید از مناطق جنگی به شلمچه و هویزه اعزام کند. هزینه بلیط قطار برای هر دانش¬آموز از تهران تا خرمشهر، سی هزار تومان است.
الف) هزینه خرید بلیط برای a دانش¬آموزان را به صورت یک عبارت جبری بنویسید.
ب) اگر مدرسه دارای 120 دانش آموز در پایه هفتم باشد، برای تهیه بلیط قطار دانش آموزان چقدر باید بپردازند؟
5- مقدار عددی عبارت های جبری را به ازای عددهای داده شده به دست آورید.
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
فعالیت
معادله
1- محیط مربعی 12 متر است. طول ضلع آن چقدر است؟
در تساوی مقابل عدد 12 را به جای چه حرفی باید قرار دهید؟ چرا؟ P=4a
چه چیزی مجهول است و باید مقدار آن را به دست آورید؟
این مقدار از حل کدام رابطه به دست آمده است؟
2- حالا می¬خواهیم ببینیم پاسخ رابطۀ 6n+7=37 چیست؟ یعنی چه عددی به جای n در نظر بگیریم تا تساوی برقرار شود؟ برای این کار به جای n عددهای مختلف را قرار دهید. درستی یا نادرستی تساوی را برسی کنید.
کدام عدد تساوی را برقرار کرد؟
پاسخ معادله چیست؟
به یک تساوی جبری که به ازای بعضی از عددها به تساوی عددی تبدیل می¬شود، «معادله» می¬گویند. برای مثال 4n=12 و 6n+7=37 معادله¬اند. جواب¬های معادله همان عددهای هستند که تساوی عددی را برقرار می¬کنند.
کار در کلاس
پاسخ معادله¬های زیر را با حدس و آزمایش پیدا کنید.
آیا حدس زدن و آزمایش کردن همیشه راه¬حل مناسبی است؟ چرا؟
فعالیت
1- به دو طرف تساوی عددی زیر عددهایی را مانند نمونه اضافه کنید. آیا باز هم تساوی برقرار است؟
چه نتیجه¬ای می گیرید؟
2- دو طرف تساوی زیر را در عددهای مختلف ضرب کنید. آیا باز هم تساوی برقرار است؟
چه نتیجه¬ای می گیرید؟
3- توضیح دهید که در هر مرحله چگونه از دو نتیجه بالا استفاده شده است تا معادله حل شود.
مراحل حل معادلۀ بالا را به صورت زیر نیز می¬توان خلاصه کرد.
کار در کلاس
معادله¬های زیر را حل کنید.
فعالیت
همان طور که در فصل اول کتاب بیان شد، راهبرد روش¬های نمادین، کاربردهای زیادی دارد. اکنون که استفاده از حروف را آموخته¬اید، مسئله زیر را به یک معادله تبدیل و آن را حل کنید.
باغبان شهرداری 100 عدد گل بنفشه داشت. او تعدادی از گل¬ها را در باغچه¬ای به مساحت 6 متر مربع در میدان شهر کاشت و در آخر هم 4 گل اضافه آورد. او به طور متوسط در هر متر مربع چند بنفشه کاشته است؟
(انتخاب مجهول) خواسته مسئله: x: تعداد بنفشه¬ها در هر متر مربع
تبدیل عبارت کلامی مسئله به تساوی جبری (تشکیل معادله):
(حل معادله):
تمرین
1- معادله¬های زیر را حل کنید.
2- فاطمه کتاب داستانی را در 6 ساعت مطالعه کرد و 10 صفحه از آن باقی ماند. اگر این کتاب 100 صفحه داشته باشد، فاطمه به طور متوسط در هر ساعت چند صفحه از آن را مطالعه کرده است؟
3- محسن برای خرید 8 مداد 4000 تومان به فروشنده داد و 800 تومان پس گرفت. قیمت آن مداد چند تومان بوده است؟
4- از یک توپ پارچۀ 30 متری 12 دست کت و شلوار دوخته شده و 6/3 متر هم باقی مانده است. برای هر دست کت و شلوار چند متر پارچه مصرف شده است؟
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
5- آیا x=2 جواب معادله است؟ چرا؟
6- آیا x=3 جواب معادلۀ x×x-3x=0 است؟ چرا؟
7- احمد و بهمن 36 جلد کتاب را صحافی کردند. احمد 6 جلد کتاب بیش از بهمن صحافی کرده است. هر کدام از آن¬ها چند جلد کتاب صحافی کرده است؟
حل سه تمرین زیر برای همه دانش آموزان الزامی نیست.
8- سه عدد صحیح زوج متوالی پیدا کنید که حاصل جمع آن 42- شود.
9- دوعدد متوالی را به گونه¬ای پیدا کنید که مجموع آن¬ها برابر 19 گردد.
10- چهار عدد صحیح فرد متوالی را به گونه¬ای پیدا کنید که مجموع آنها عدد 80- گردد.
مرور فصل 3
مفاهیم و مهارت¬ها
در این فصل واژه¬های زیر به کار رفته¬اند. مطمئن شوید که می¬توانید با جملات خود آن¬ها را تعریف کنید. برای هر کدام مثال بزنید.
* الگوی عددی * عبارت جبری * متغیّر * جملات متشابه * معادله
در این فصل روش¬های اصلی زیر مطرح شده¬اند. با یک مثال هر کدام را توضیح دهید و در دفتر خود یک خلاصه درس بنویسید.
* نوشتن جملۀ nام یک الگو * پیدا کردن جواب معادله با حدس زدن
* تبدیل عبارت¬های کلامی به عبارت¬های جبری * تشکیل معادله و تبدیل مسئله¬های یک معادله
* نوشتن محیط و مساحت شکل¬ها با عبارت جبری * پیدا کردن مقدار عددی یک عبارت جبری
* ساده کردن عبارت¬های درس با جمع و تفریق جملات متشابه * مفهوم معادله و جئاب معادله
* ضرب عدد در پرانتز * روش حل معادله
* ساده کردن عبارت و سپس محاسبۀ مقدار عبارت جبری
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
کاربرد
مهم¬ترین کاربرد این درس، حل مسئله با کمک راهبرد روش های نمادین (تشکیل معادله) و بیان جبری الگوها و خاصیت¬ها و قوانین است. از این درس در فصل¬های بعدی استفاده زیادی از جمله برای بیان رابطه¬های مربوط به مساحت و حجم خواهد شد.
تمرین¬های ترکیبی
در صورتی که تمرین¬های ترکیبی زیر را بتوانید انجام دهید، مطمئن می¬شوید این فصل را به خوبی آموخته-اید.
1- مقدار عبارت جبری زیر را به ازای x=-1 و y=-2 پیدا کنید.
2- معادله زیر را حل کنید.
3- شخصی با سوزاندن 3500 کالری، 45/0 کیلوگرم از وزنش را کم می¬کند. میزان کالری¬ای که فرد باید در هر روز بسوزاند تا در 2 هفته 8/1 کیلوگرم از وزنش کم شود، چقدر است؟
4- یک مسئله بنویسید که متناظر با معادله مقابل باشد. 2x-1=7
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
فصل 4
هندسه و استدلال
به اطراف خود نگاه کنید. چند شکل هندسی می¬بینید؟ ما در دنیایی از شکل ها و حجم¬ها زندگی می¬کنیم. انواع خطوط نیز به صورت¬های مختلف در زندگی ما دیده می¬شوند. خط،نقطه، زاویه، سطح و حجم از عناصر اصلی علم هندسه¬اند.
روابط بین پاره خط¬ها
روابط بین زاویه¬ها
تبدیلات هندسی
شکل¬های مساوی )هم¬نهشت(
روابط بین پاره¬خط¬ها
در ریاضیات برای نام¬گذاری شکل¬ها از حروف انگلیسی استفاده می¬کنیم. به طور معمول نقطه را با حروف بزرگ انگلیسی نام¬گذاری می¬کنیم و برای نام¬گذاری امتداد خط که در شکل با پیکانه نشان می¬دهیم از حروف کوچک استفاده می¬کنیم.
طول یک پاره خط را با قراردادن یک پاره خط کوچک در بالای نام آن نمایش می دهیم. برای مثال (AB) ̅ یعنی طول پاره¬خط AB
فعالیت
1- مانند نمونه¬ها شکل را با حروف انگلیسی نام¬گذاری کنید.
2- در شکل زیر نام خط¬ها، نیم خط¬ها و پاره خط¬ها را بنویسید و در صورت لزوم از راهبرد الگوسازی استفاده کنید.
خط:
نیم¬خطم:
پارخ¬خط:
3- در شکل مقابل نقاط A، B و C روی یک خط قرار دارند. رابطه زیر را کامل کنید.
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
4- در شکل زیر نقاط A، B و C روی یک خط قرار دارند.
نقاط A، B و C یک مثلث تشکیل داده¬اند. این مثلث ABC نام دارد و آن را به صورت ∆ABC یا نمایش می¬دهیم. رابطه¬های زیر را کامل کنید.
یک مثلث دلخواه دیگر رسم کنید و آن را ABC بنامید.
آیا همین رابطه¬ها در آن مثلث هم برقرار است؟
کار در کلاس
1- مانند نمونه رابطه¬های دیگری را بنویسید که در همه شکل¬ها برقرار باشد.
2- می¬دانیم (cm مخفف سانتی¬متر است.)
یک رابطۀ جبری بنویسید و با جایگزین کردن عددها، طول پاره¬خط CD را به دست آورید.
فعالیت
1- پاره خط¬های مساوی را به صورت روبه¬رو در شکل مشخص می¬کنیم.
علامت¬ها نشان می¬دهند که: (AB) ̅=(AB) ̅
در شکل مقابل M وسط پاره¬خط AB است.
اندازۀ کدام دو پاره¬خط با هم مساوی¬اند؟ ـــــــــ = ــــــــــ
تساوی این دو پاره¬خط را با علامت¬گذاری روی شکل نشان دهید. تساوی¬های زیر را با نوشتن عدد مناسب کامل کنید.
2- در شکل زیر پاره¬خط¬های AB، BC، CD و DE با هم مساوی¬اند. طول کدام پاره¬خط¬ها برابر 3(AB) ̅ است؟
طول کدام پاره¬خط¬ها برابر 2(AB) ̅ است؟
چند پاره¬خط در شکل روبه¬رو دیده می¬شود؟
3- با توجه به پاره¬خط¬هایی که در شکل زیر می¬بینید، اگر بدانیم ، رابطه¬های زیر را کامل کنید. (این علامت یعنی نتیجه می¬گیریم):
4- مثلث ABC متساوی¬الساقین است؛ یعنی: (AB) ̅=(AC) ̅
نقطۀ M وسط AB و نقطۀ N وسط AC است.
چرا (AN) ̅=(AM) ̅؟
کار در کلاس
1- اگر پاره¬خط¬های AB، BC، CD و DE با هم برابر باشند، تساوی¬ها را با نوشتن عدد مناسب کامل کنید.
2- در شکل مقابل نقاط A، B، C و D روی یک خط قرار گرفته¬اند.
می¬دانیم: (AB) ̅=(CD) ̅
کدام پاره¬خط هم اندازۀ AC است؟ ـــــــــــ چرا؟
تمرین
1- با رسم شکل¬های مناسب به سؤال¬های زیر پاسخ دهید.
الف) از یک نقطه چند خط می¬گذرد؟ ب) از یک نقطه چند خط راست می¬گذرد؟
ج) از دو نقطه چند خط از (انواع مختلف) می¬گذرد؟ د) از دو نقطه چند خط راست می¬گذرد؟
2- یک خط رسم کنید و نقاط A، B، C و D را طوری روی آن نام¬گذاری کنید که رابطۀ زیر درست باشد.
3- اگر روی یک خط راست ١٠ نقطه بگذارید، چند نیم خط به وجود می¬آید که سر آن¬ها روی این نقاط باشد؟ چرا؟
4- نقطۀ C وسط پاره¬خط AB، نقطۀ D پاره¬خط AC و نقطۀ E وسط پاره¬خط AD است. (AB) ̅ چند برابر (AE) ̅ است؟
5- در شکل روبه¬رو یک مربع و یک مثلث متساوی¬الاضلاع دیده می¬شود.
چرا
6- دو خط کش ٢٠ سانتی¬متری را مانند شکل روبه¬رو، روی یک صفحه کاغذ قرار داده¬ایم. طول این صفحه چند سانتی¬متر است؟
7- اندازۀ قد علی را با a، اندازۀ قد حسن را با b و اندازۀ قد حسین را با c نشان می¬دهیم. رابطۀ زیر را کامل کنید و نتیجه را به فارسی بنویسید.
رابطه بین زاویه¬ها
زاویه مقابل نام¬گذاری شده و به چند صورت خوانده می شود. چرا از حروف کوچک و بزرگ استفاده شده است؟
فعالیت
1- با انواع زاویه ها در سال گذشته آشنا شده اید، زاویه ها را نام گذاری کنید و نوع هرکدام را مشخص کنید.
2- تساوی بین زوایه¬ها را کامل کنید.
3- دو زاویه مساوی را به صورت روبه رو در شکل مشخص می¬کنیم: علامت¬ها نشان می¬دهند که:
4- در شکل مقابل Ox نیمساز زاویۀ aO ̂b است. زاویۀ O ̂_1 با کدام زاویه مساوی است؟ تساوی این دو زاویه را با علامت¬گذاری روی شکل نشان دهید.
5- در شکل مقابل دو خط یکدیگر را در نقطۀ O ̂ قطع کرده¬اند.
می¬دانیم O ̂_1=70° است. اندازه زاویه¬های دیگ را با نوشتن یک تساوی پیدا کنید.
1- زاویه¬های O ̂_1، O ̂_2، O ̂_3 و O ̂_4 همه با هم برابرند. جاهای خالی را با عدد مناسب کامل کنید.
2- برای زاویه¬های متمم و مکمل تساوی بنویسید.
فعالیت
1- می دانیم در هر مثلث، مجموع زاویه ها برابر 180° است.
مثلث ها را با توجه به اندازه زاویه هایشان به سه دسته تقسیم می کنیم:
مثلث هایی که هر سه زاویه آنها تند است.
مثلث هایی که یک زاویه راست دارند.
مثلث هایی که یک زاویه باز دارند.
چرا مثلث نمی تواند دو زاوی راست داشته باشد؟
2- می خواهیم در هر قسمت جدول مقابل یک مثلث رسم کنیم.
در کدام قسمت ها نمی توانیم مثلثی رسم کنیم؟
در قسمت هایی که می توانیم مثلث رسم کنیم، یک مثلث بکشید.
3- هریک از شکل های زیر یک چند ضلعی¬اند.
چند ضلعی¬هایی که هیچ زاویه بزرگ تر از 180° ندارند، محدّب نامیده می شوند.
به چند ضلعی¬ای که دست کم یک زاویهٔ بزرگ تر از 180° داشته باشد، چند ضلعی مقعر می¬گویند.
چند ضلعی های مقعر (کاو) و محدّب (کوژ) را در شکل زیر مشخص کنید.
4- به چندضلعی¬هایی که همۀ ضلع¬ها و زاویه¬هایشان با هم مساوی است، چند ضلعی منتظم گفته می¬شود. کدام شکل در فعالیت قبل چندضلعی منتظم بود؟
تمرین
1- یک مثال برای هریک از زمان هایی بنویسید که عقربه بین ساعت شمار و دقیقه شمار زاویه راست، باز، تند و نیم صفحه را نشان دهد.
2- اندازۀ زاویه¬های x و y را در شکل¬های زیر پیدا کنید.
3- در شکل¬های مقابل می¬دانیم زاویه¬های xO ̂z، tO ̂y، 90° هستند.
چگونه می¬توانید نتیجه بگیرید که: tO ̂z= xO ̂y ؟
4- در شکل مقابل اندازۀ xA ̂z، برابر 120 درجه است. زاویۀ xA ̂y، چه کسری از xA ̂z، است؟
5- شکل¬های زیر چه شباهت هایی با هم دارند؟ چه تفاوت هایی با هم دارند؟
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
تبدیلات هندسی (انتقال، تقارن، داوران)
فعالیت
1- یک کاغذ شفاف روی شکل A قرار دهید و این شکل را روس کاغذتان بکشید، کاغذ شفاف را بدون تغییر جهت روی صفحه حرکت دهید تا تصویر آن روی شکل B قرار بگیرد.
بدین ترتیب تصویر شکل A را روی صفحه انتقال داده¬اید.
2- دوباره کاغذ پوستی خود را طوری روی صفحه قرار دهید که تصویری کشیده¬اید، روی شکل A قرار بگیرد.
کاغذتان را از روی خط تقارن تا کنید. بدین ترتیب تصویر شکل A روی کدان شکل قرار می¬گیرد.
این شکل قرینۀ شکل A نسبت به خط تقارن است. قرینۀ شکل B را هم نسبت به خط تقارن رسم کنید و آن را D بنامید.
کار در کلاس
1- به اندازه و جهت شکل های سفید نگاه کنید. کدام یک از شکل¬¬ها، انتقال یافته شکل آبی است؟ این شکل را هاشور بزنید.
2- کدام شکل قرینه شکل آبی است؟ خط تقارن متناسب با این تقارن را رسم کنید.
وقتی شکلی را روی صفحه انتقال می دهیم، تصویر به دست آمده مساوی و هم جهت شکل اولیه است. وقتی قرینه شکلی را نسبت به یک خط پیدا می کنیم، تصویر به دست آمده مساوی آن شکل است؛ امّا جهت آن تغییر می کند.
فعالیت
1- یک کاغذ پوستی روی شکل A قرار دهید و این شکل را روی آن بکشید. با استفاده از یک مداد کاغذ پوستی خود را در مرکز دوران شکل، روی صفحه کتاب ثابت کنید و آرام کاغذ را روی کتاب بچرخانید و به حرکت تصویر در صفحه نگاه کنید.
2- اگر کاغذ پوستی را 180 درجه بچرخانید، تصویر شکل A مانند شکل روبه¬رو در صفحه قرار می¬گیرد. این تصویر حاصل دوران 180 درجه¬ای شکل A حول مرکز دوران است.
3- باز هم کاغذ پوستی را روی شکل قرار دهید و با استفاده از آن تصویر حاصل تز دوران 180 درجۀ شکل A حول مرکز دوران جدید را بسازید.
4- با کمک کاغذ پوستی شکل A را حول مرکز دوران 90 درجه در جهت عقربه¬های ساعت چرخانده¬ایم. تصویر شکل A روی شکل B قرار گرفته است. شکل B را حول مرکز دوران، 90 درجه در جهت عقربه¬های ساعت بچرخانید. شکل حاصل از این دوران را رسم کتید و آن را C بنامید.
چرا در دوران ٩٠ درجه لازم است جهت دوران را مشخص کنیم؛ امّا در دوران ١٨٠ درجه این کار لازم نیست؟
تمرین
1- الف) شکل A را 90 درجه حول نقطۀ O در جهت عقربه¬های ساعت بچرخانید و شکل حاصل را B بنامید.
ب) قرینۀ A را نسبت به خط d رسم کنید و آن را C بنامید.
ج) آیا هر سه با هم مساوی¬اند؟
2- الف) کدام شکل از دوران 180 درجه شکل 1 در جهت عقربه های ساعت حول مرکز دوران به دست آمده است؟
ب) کدام شکل از دوران ١٨٠ درجه شکل 4 حول مرکز دوران به دست آمده است؟
3- همه شکل های مقابل با هم مساوی¬اند.
الف) کدام شکل ها انتقال یافته شکل رنگی هستند؟
ب) کدام شکل ها دوران یافته شکل رنگی هستند؟
ج) کدام شکل ها قرینه شکل رنگی نسبت به یک خط هستند؟
٤ در هر مورد چه تبدیلی انجام شده است؟ انتقال، تقارن محوری یا دوران؟
الف) A و B تبدیل شده است.
ب) A به C تبدیل شده است.
ج) B به E تبدیل شده است.
د) D به C تبدیل شده است.
5- در هر مورد با دو تبدیل مختلف می¬توان A را بر B منطبق کرد. این دو تبدیل را نام ببرید.
6- در شکل مقابل کدام دو شکل مساوی، یک شکل و تبدیل یافته آن تنها با یک تبدیل (انتقال، تقارن یا دوران) را نشان می¬دهد؟
شکل¬های مساوی (هم¬نهشت)
فعالیت
1- الف) هر شکل با یک تبدیل، به شکل بعدی تبدیل شده است. روی هر پیکانه نوع تبدیل انجام شده (انتقال، تقارن یا دوران) را بنویسید.
ب) آیا شکل A با شکل H مساوی است؟ چرا؟
٢ اگر بتوانیم شکلی را با یک یا چند تبدیل (انتقال، تقارن یا دوران) در صفحه بر شکل دیگر منطبق کنیم، می گوییم این دو شکل باهم هم نهشت (مساوی) اند.
دو شکل مقابل با هم هم نهشت¬اند.
شک ضلع و یک زاویه از شکل A مشخص شده است.
ضلع و زاویۀ مساوی (متناظر) با آن¬ها در شکل B را با علامت¬گذاری مشخص کنید.
یک ضلع و یک زاویه از شکل A مشخص شده است.
ضلع و زاویۀ مساوی (متناظر) با آن¬ها در شکل B را با علامت¬گذاری مشخص کنید.
٣ دو شکل مقابل هم نهشت¬اند. این عبارت را در ریاضی به صورت ABCDE ≅ HGFKJ نمایش می دهیم.
در دو شکل هندسی هم¬نهشت، اجزای متناظر دو به دو با هم برابرند.
به چگونگی نمایش برابری ضلع ها و زاویه ها در دو شکل بالا توجه کنید.
کار در کلاس
1- مثلث های هم¬نهشت را در شکل بیابید و به زبان ریاضی بنویسید.
2- در شکل مقابل دو مثلث هم نهشت دیده می¬شود.
ضلع¬ها و زاویه¬های مساوی دو شکل را با علامت گذاری مشخص کنید. تساوی اجزای متناظر این دو مثلث را کامل کنید.
فعالیت
1- با انجام تبدیلات متوالی روی یک مثلث، قسمتی از صفحه را پوشانده¬ایم. مثلث¬هایی را که از انتقال مثلث رنگی به دست آمده¬اند، رنگ کنید.
هریک از مثلث¬های سفید را می توان با دوران ١٨٠ درجه یکی از مثلث های رنگی به دست آورد.
زاویه¬های مساوی در همه مثلث¬ها را با شماره¬گذاری آن¬ها مشخص کنید. آیا همه این مثلث ها با هم مساویند؟
2- با انجام تبدیلات متوالی روی یک چهارضلعی قسمتی از صفحه را پوشانده¬ایم.
چهارضلعی¬¬هایی را که از انتقال چهارضلعی رنگی به دست آمده¬اند، رنگ کنید. با چه تبدیلی می¬توان چهارضلعی¬های سفید را به دست آورد؟
ضلع¬ها و زاویه¬های مساوی را با علامت گذاری مشخص کنید.
آیا همه این چهارضلعی¬ها با هم مساوی¬اند؟
تمرین
1- در شکل مقابل ضلع¬های دو چهارضلعی، دو به دو با هم برابرند.
الف) با علامت¬گذاری مناسب تساوی ضلع¬ها را نمایش دهید.
ب) آیا این دو چهارضلعی با هم مساوی¬اند؟
2- می¬خواهیم شکل B را طوری رسم کنید که بتوانیم با دو تبدیل متوالی، شکل A را بر شکل C منطبق کنیم. شکل B را رسم کنید و روی هر پیکانه نوع تبدیل انجام شده را بنویسید.
3- به کمک کاغذ پوستی شکل¬های مساوی را پیدا کنید و تساوی شکل ها را به زبان ریاضی بنویسید.
4- با انجام تبدیلات متوالی روی یک هشت ضلعی و مربع، قسمتی از صفحه را پر کرده¬ایم.
به چند طریق می¬توان تنها با یک تبدیل هشت¬ضاعی رنگی را بر شکل C منطبق کرد؟
5- شکل زیر قسمتی از کاشی¬کاری یک بنای قدیمی را نشان می¬دهد.
الف) چگونه می¬توان با دو تبدیل متوالی A را بر شکل B منطبق کرد؟
ب) با ادامه الگوی ایجاد شده، صفحه را پر کنید.
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
مرور فصل 4
مفاهیم و مهارت¬ها
دراین فصل واژه¬های زیر به کار رفته¬اند. مطمئن شوید که می توانید با جملات خود آن¬ها را تعریف کنید. برای هر کدام مثال بزنید.
تبدیل¬های هندسی شکل¬های هم¬نهشت اجزای متناظر
در این فصل روش¬های اصلی زیر مطرح شده اند. با یک مثال هر کدام را توضیح دهید و در دفتر خود یک خلاصه درس تهیه کنید.
* نام گذاری پاره خط، نیم خط وخط * نام گذاری زاویه
* نوشتن رابطه بین پاره خط¬ها * نوشتن رابطه بین زاویه¬ها
* نتیجه¬گیری از چند تساوی درست * دلیل تساوی دو زاویه متقابل به رأس
* انتقال یک شکل * پیدا کردن قرینه یک شکل
* پیدا کردن دوران یافته یک شکل * نوشتن تساوی اجزاء متناظر دو شکل
کاربرد
کاربرد این درس را در فصل هفتم (بردار) خواهید دید. ضمن آنکه در کشیدن شکل¬های هندسی، گرافیک رایانه¬ای، طراحی و …نیز کاربرد دارد.
تمرین¬های ترکیبی
در صورتی که تمرین¬های ترکیبی زیر را بتوانید انجام دهید، مطمئن می¬شوید که این فصل را به خوبی آموخته¬اید.
1- چرا C ̂=A ̂_1 است؟
2- قرینۀ شکل مقابل را نسبت به پاره¬خط BC پیدا کنید.
دوران یافته شکل جدید را نسبت به نقطۀ C با دوران 90° در جهت حرکت عقربه¬های ساعت پیدا کنید. اجزاء متناظر شکل اول و آخر را با علامت¬گذاری مشخص کنید.
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
فصل 5
شمارنده¬ها و اعداد اول
دسته¬بندی کردن، به¬ویژه ساختن دسته¬های مساوی و قابلیت تقسیم از مفاهیم با کاربرد در زندگی روزمره¬اند. وقتی سربازها در دسته¬های منظم شدۀ رژه قرار دارند، تعداد آن¬ها باید بر تعداد ردیف¬ها و ستون¬ها قابل قسمت باشد.
عدد اول
شمارندۀ اول
بزرگ¬ترین شمارندۀ مشترک
کوچک¬ترین مضرب مشترک
عدد اول
فعالیت
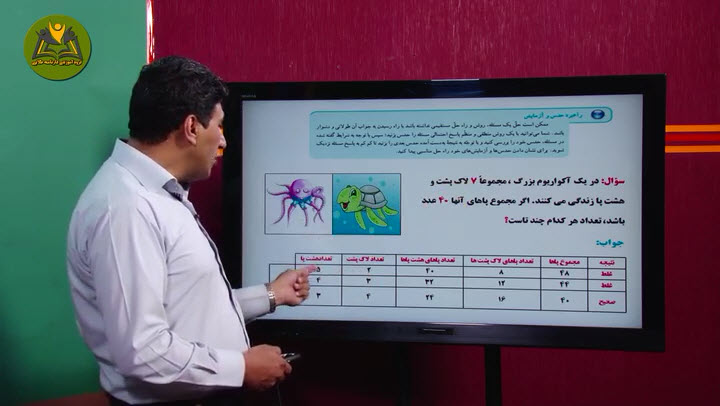
1- دانش آموزان یک مدرسه در کلاس¬های ورزشی ثبت نام کرده¬اند. تعداد ثبت نام شده¬ها و تعداد نفرات هر تیم در آن رشته در جدول زیر مشخص شده است. در کدام رشته ورزشی تعداد ثبت نام شده¬ها مناسب است؟ چرا؟
در کدام رشته تعداد ثبت نام شده ها مناسب نیست؟ چرا؟
با کمترین جابه جایی نفرات، پیشنهادی ارائه کنید تا تعداد نفرات تمام رشته ها مناسب شوند.
2- عدد ٦ را مانند نمونه به صورت ضرب دو عدد طبیعی بنویسید و معنی کنید.
3- عدد 10 را مانند نمونه تقسیم کنید و یک تساوی بنویسید و آن را معنا کنید )تقسیم ها نباید باقی مانده بیاورند(.
4- مانند نمونه 12 دایره را به دسته های مساوی تقسیم کنید؛ یعنی مشخص کنید 12 را چند تا چند تا می شود شمرد. به این ترتیب شمارنده های عدد ١٢ به دست می¬آید.
کار در کلاس
1- با یکی از روش های بالا شمارنده های هر عدد را مشخص کنید.
:شمارنده¬های 15 : شمارنده¬های 14
: شمارنده¬های 8 : شمارنده¬های 9
2- عدد ٢، شمارنده 4 است. 4 هم شمارنده 12 است. آیا می توان نتیجه گرفت که 2 شمارنده 12 هم است؟ چرا؟
3- به طور کلی اگر a شمارندۀ b باشد، b هم شمارندۀ c باشد، آیا می¬توان نتیجه گرفت که a شمارندۀ c هم است؟ چرا؟
فعالیت
1- جدول زیر را کامل کنید. شمارنده های عدد را از کوچک به بزرگ بنویسید.
با دیدن این جدول چه نتیجه ای می توان گرفت؟
عدد ______________ شمارنده همه اعداد است.
کوچک ترین شمارنده هر عدد ______________ است.
بزرگ ترین شمارنده هر عدد ______________ است.
همه شمارنده های یک عدد ______________ آن عدد هستند.
بعضی از عددها فقط ______________
هر عدد بزرگ تر از ١ حداقل ______________ دارد.
2- برای عدد 7 از روش های ضرب یا تقسیم کردن یا دسته بندی استفاده کرده و شمارنده های آن را پیدا کنید.
به عددهایی مثل 5، 13 و 7 که فقط شمارنده دارنده و آن دو شمارنده، عدد یک و خود آن عدد است، عدد اول می¬گویند.
کار در کلاس
1- مانند نمونه عددها را به حاصل ضرب دو عدد غیر از یک بنویسید.
کدام عددها را نمی توان به صورت ضرب دو عدد غیر از یک نوشت؟
آیا می¬توان گفت هر عددی که به صورت ضرب دو عدِد بزرگ تر از یک نوشته شود، اول نیست؟
2- با قاعده بخش¬پذیری بر 2، 3، 5 که در دبستان آموخته¬اید و یا روش¬های بالا، مشخص کنید کدام یک از عددهای طبیعی کمتر از30 ، اول هستند. دور آن¬ها را خط بکشید. عددهایی را که اول نیستند، به صورت بالا با ضرب دو عدد غیر از یک نشان دهید.
1- آیا عدد 17 شمارنده 247 است؟ چرا؟
2- آیا اگرعددی بر 3 بخش پذیر بود، می¬توان گفت که 3 شمارنده آن است؟
3- چهار عدد بنویسید که 5 شمارنده آن¬ها باشد.
345 ، 924 ، 555 ،360
4- کدام یک از عددهای روبه¬رو بر 15 بخش پذیر است؟ چرا؟
5- تمام شمارنده¬های عددهای زیر را بنویسید.
6- جملات درست را با و جملات نادرست را با × مشخص کنید. دلیل نادرست بودن آن جمله را بنویسید.
* عدد 29 اول است. * هر عدد حداقل 2 شمارنده دارد.
* تمام عددهای اول، فرد هستند؛ چون اگر زوج باشند، عدد 2 شمارنده آنها می شود.
* اگر عددی غیر از خودش و یک شمارنده دیگری داشت، حتماً اول نیست.
7- در کلاس 4 گروه 3 نفره و 6 گروه 4 نفره وجود دارد.
دانش¬آموزان این کلاس را در چند حالت می¬توان به گروه¬هایی با تعداد مساوی که تعداد نفرات هر گروه بین 2 و 7 نفر باشند، تقسیم کرد؟
8- وقتی می¬نویسیم 3×6=18، آیا می¬توان نتیجه گرفت که هم 3 و هم 6 شمارندۀ¬های 18 هستند؟ چرا؟
آیا می¬توان نتیجه گرفت که همیشه تعداد شمارنده¬های یک عدد زوج است؟
9- آیا حاصل ضرب دو عدد اول می¬تواند عددی اول باشد؟ چرا؟
10- هر عبارت را کامل کنید.
* مجموع دو عدد طبیعی فرد همیشه عددی ___________ است.
* مجموع دو عدد طبیعی زوج همیشه عددی ___________ است.
* مجموع یک عدد زوج و یک عدد فرد همیشه عددی ___________ است.
پس از تکمیل کردن جمله های فوق (می¬توانید با حدس و آزمایش جمله ها را کامل کنید) به سؤال زیر پاسخ دهید.
* آیا حاصل جمع دو عدد اول همواره یک عدد اول است؟
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
شمارندۀ اول
فعالیت
1- تمام شمارنده های عددهای زیر را بنویسید.
: شمارنده¬های 35 : شمارنده¬های 12
: شمارنده¬های 9 : شمارنده¬های 14
در هر قسمت، زیر شمارنده هایی که عدد اول اند، خط بکشید.
شمارنده های اول 35 چه عددهایی اند؟ شمارنده اول عدد 9 چه عددی است؟
2- مانند نمونه هر عدد را به صورت ضرب دو عدد بنویسید. این کار را آن قدر ادامه دهید تا به شمارنده¬های اول آن عدد برسید.
3- با توجه به نمودارهای درختی بالا می¬توان عددها را به صورت ضرب عددهای اول نوشت (تجزیه کرد):
شمارنده های اول، عددهای اولی هستند که با استفاده از حاصل ضرب و تکرار آن¬ها، می توان عددهای مختلفی را به دست آورد.
مانند: 12=3×2×2.
به نظر شمار عدد 7 چند شمارندۀ اول دارد؟ چرا؟
کار در کلاس
با شمارنده¬های اول 2 و 3 عددهای مختلف را با ضرب کردن بسازید. مانند نمونه¬ها بنویسید.
ویژگی عددهای به دست آمده این است که شمارنده های اول آن¬ها عددهای 2 و 3 هستند.
فعالیت
1- شمارنده های اول عددهای زیر را با رسم نمودار درختی پیدا کنید و آن¬ها را به صورت ضرب شمارنده اول بنویسید.
8 36 100
=8 =36 =100
2- با راهبرد الگوسازی می¬توان تمام شمارنده¬های یک عدد را پیدا کرد. در زیر تمام شمارنده¬های عدد ١٢ با توجه به تجزیه آن پیدا شده است. به همین روش تمام شمارنده¬های عدد ١٠٠ را پیدا کنید.
کار در کلاس
1- در دوره دبستان آموختید که چگونه کسرها را ساده کنید. به مثال های زیر توجه کنید.
با تجزیه کردن (نوشتن عدد به صورت ضرب عامل¬های اول) عددهای صورت و مخرج، کسرها را تا حد امکان ساده کنید. در واقع شمارنده های مشترک صورت و مخرج را ساده کنید.
2- مساحت یک مستطیل که طول و عرض آن عددهای طبیعی اند، 18 شده است.تمام حالت هایی را که طول و عرض مستطیل می توانند داشته باشند، بنویسید.
طول و عرض این مستطیل چه ارتباطی با مساحت آن دارند؟
تمرین
1- شمارنده های اول صورت یک کسر 2 و 3 هستند. شمارنده های اول مخرج آن کسر 5 و 7 هستند. آیا این کسر ساده می شود؟ چرا؟
2- سه کسر بنویسید که پس از ساده شدن برابر 3/5 شود.
3- با شمارنده های اول 2و 3 چند عدد تولید می شود که بین 30 و 50 باشد؟
4- عدد a پس از تجزیه به صورت مقابل در آمده است. a=2×2×3×5×5
شمارنده¬های اول آن چه عددهایی¬اند؟ 4 شمارندۀ این عدد را بنویسید که اول نباشد.
5- عدد b پس از تجزیه به صورت مقابل درآمده است.
شمارنده¬های اول آن چه عددهایی¬اند؟
6- عددهای زیر را با رسم نمودار درختی تجزیه کنید و شمارنده های اول آنها را مشخص کنید.
297 104 180
7- عددهای 7 و 5 و 13 اول اند. شمارنده های اول آنها را بنویسید. براساس آن تعریف دیگری برای عددهای اول ارائه کنید.
8- جملات درست را با و نادرست را با × مشخص کنید. دلیل نادرستی را توضیح دهید.
الف) تمام عددها شمارنده اول دارند.
ب) اگر عددی زوج باشد، یکی از شمارنده¬های اولش 2 است.
ج) هیچ عددی پیدا نمی¬شود که 5 شمارنده اول داشته باشد.
د) تعداد عددهای اول بی¬پایان¬اند.
9- الگوهای شکل¬ها را به الگوهای عددی تبدیل کنید. جملۀ nام هر کدام را بنویسید.
بزرگ¬ترین شمارنده مشترک
فعالیت
1- قرار است دانش آموزان سال اول یک مدرسه به اردو بروند. آنها می¬خواهند در اردو چادر بزنند. تعداد افراد چادرها باید مساوی باشند. کلاس اول الف 30 دانش¬آموز دارد. در این کلاس از چادرهای چند نفره می¬توان استفاده
کرد؟ چرا؟
کلاس اول ب، 36 دانش آموز دارد. برای این کلاس چه چادرهایی می توان بر پا کرد؟ چرا؟
اگر قرار باشد یک نوع چادر، برای هر دو کلاس تهیه کنیم، چادرهای چند نفره مناسب است؟ چرا؟ اگر قرار باشد از چادر مشترک برای دو کلاس استفاده شود و تعداد دانش آموزان یک چادر بیشترین تعداد باشد تا چادر کمتری تهیه شود، چادر چند نفره مناسب است؟
2 دو عدد 24 و 18 را در نظر بگیرید. می خواهیم بزرگ ترین شمارندهٔ مشترک دو عدد را پیدا کنیم.
امید از روش زیر استفاده کرد:
= شمارنده¬های مشترک دو عدد 18، 9، 6، 3، 2، 1 : تمام شمارنده¬های 18
= بزرگ¬ترین شمارندۀ مشترک دو عدد : تمام شمارنده¬های 24
احمد از روش زیر استفاده کرد. او ابتدا عددها را به صورت ضرب شمارنده های اول نوشت.
24=2×2×2×3 18=2×3×3
سپس حاصل ضرب قسمت های مشترک آنها را مشخص کرد تا بزرگ ترین شمارندهٔ مشترک مشخص شود.
شمارنده های یک عدد را مقسومٌ علیه های آن نیز می گویند؛ بنابراین بزرگ ترین شمارندۀ مشترک دو عدد همان بزرگ ترین مقسومٌ¬علیه مشترک است که به اختصار آن را ب.م.م می¬نویسند. ب.م.م دو عدد a و b را به صورت (b و a) نشان می¬دهند. مانند:
6= (24 و 18)
آیا می توانید بگویید در فعالیت بالا احمد از چه روشی استفاده کرده است؟
کار در کلاس
1- با نوشتن تمام شمارنده های دو عدد ب.م.م آنها را پیدا کنید.
= (30 و 20) = (12 و 14)
2- با تجزیهٔ عددها به شمارنده های اول ب.م.م دو عدد را پیدا کنید.
= (30 و 42) = (36 و 48)
فعالیت
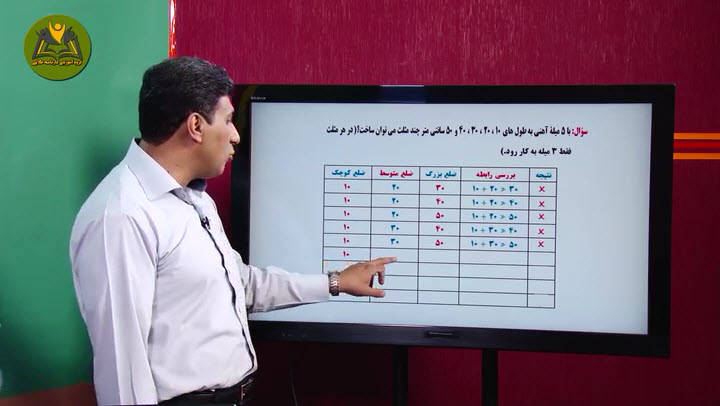
1- می خواهیم یک قاب مستطیلی به طول 16 و عرض 12 سانتی متر را با کاشی های مربعی پر کنیم.ضلع این کاشی مربعی چه عددهایی می تواند باشد؟ چرا؟
اگر بخواهیم کاشی های مصرف شده کمترین تعداد باشند (ضلع کاشی باید بزرگ باشد)، چه عددی برای ضلع کاشی مناسب است؟چرا؟
اگر بخواهیم کاشی های مصرف شده بیشترین تعداد باشند (ضلع کاشی کوچک ترین عدد باشد) چه عددی برای ضلع کاشی مناسب است؟ چرا؟
2- یک جعبه دستمال کاغذی به شکل مکعب مستطیل داریم که طول آن 25 ، عرض آن 12 و ارتفاعش 5 سانتی¬متر است. تعیین کنید چند عدد از این جعبه¬ها در یک کارتن مکعب مستطیل به ابعاد 50، 24 و 30 سانتی¬متر جا می¬گیرد.
در این مسئله ابعاد کارتن چه ارتباطی با ابعاد جعبه دستمال دارند؟ با توجه به این ارتباط شکل زیر را کامل کنید تا مشخص شود چند جعبه در این کارتن جا گرفته است؟
کار در کلاس
عددهای زیر تجزیه شده اند، ب.م.م های خواسته شده را به دست آورید.
تمرین
1- دو ظرف به گنجایش 12 و 18 لیتر داریم. می خواهیم با یک پیمانه که هر بار پر و خالی می¬شود، دو ظرف را به طور کامل پر کنیم. کدام پیمانه ها برای این کارمناسب است؟ بزرگ¬ترین پیمانه کدام است؟
2- یک مکعب مستطیل به ابعاد 12 و 36 و 28 سانتی متر را با مکعب های مساوی پر کرده¬ایم. بزرگ¬ترین ضلع این مکعب چه عددی است؟ در این صورت چند مکعب در این مکعب مستطیل جا می¬شود؟
3- برای درستی جملات زیر دلیل بیاورید.
اگر دو عدد b و a اول باشند، ب.م.م آن¬ها عدد یک می¬شود. 1= (b و a)
اگر عددی بر عدد دیگری بخش¬پذیری باشد، عدد کوچک¬تر ب.م.م دو عدد است.
کوچک ترین مقسومٌ¬علیه مشترک (یا شمارندهٔ مشترک) هر دو عدد 1 است.
4- ابتدا عددهای صورت و مخرج را تجزیه کنید، سپس کسرها را ساده کنید.
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
5- ب.م.م عددهای زیر را محاسبه کنید.
6- برای جملات درست زیر 2 مثال بزنید.
* n= (n و n)
* ب.م.م دو عدد a و b شمارندۀ دو عدد a و b است.
* اگر عدد a اول باشند، ب.م.م a و عدد دیگر مثل b یا یک می¬شود یا خود a.
کوچک¬ترین مضرب مشترک
فعالیت
1- مضرب های صحیح یک عدد از ضرب آن در عددهای صحیح به دست می آید. مضرب های صحیح 3 را کامل کنید.
2- مضرب¬های طبیعی یک عدد از ضرب آن در عددهای طبیعی به دست می¬آید.
مضرب های طبیعی را به اختصار مضرب می گوییم. مضرب های عددهای زیر را بنویسید.
در این نحوهٔ نوشتن علامت … به چه معناست؟
کار در کلاس
1- به سؤال های زیر پاسخ دهید:
اولین مضرب 7: سومین مضرب 6: دهمین مضرب 9:
80 چندمین مضرب 8 است؟ 24 چندمین مضرب 6 است؟
36 چندمین مضرب 2 است؟ 144 چندمین مضرب 6 است؟
2- آیا تعداد شمارنده¬های یک عدد محدود است؟
تعداد مضرب¬های یک عدد چطور؟
فعالیت
در یک بازی رایانه¬ای مهرۀ A، 6 تا 6 تا حرکت می¬کند و مهرۀ B، 4 تا 4 تا حرکت می¬کند. در شروع بازی هر دو مهره روی هدد صفرند. در کدام عدد این دو مهره دوباره کنار هم قرار می¬گیرند؟
: مضارب مشترک : مضارب A
: کوچک¬ترین مضرب مشترک : مضارب B
کوچک¬ترین مضرب مشترک دو عدد، اولین مضرب مشترک آن دو عدد است. مضرب¬های مشترک بعدی را با داشتن اولین مضرب مشترک می¬توان پیدا کرد. کوچک¬ترین مضرب مشترک دو عدد a و b را به طور اختصار ک.م.م می¬گویند و به صورت [b و a] نمایش می¬دهند.
به عنوان نمونه 12= [4 و 6]
فعالیت
1- ک.م.م دو عدد 12 و 18 را پیدا کنید.
: مضارب 18
: مضارب 12
= [12 و 18] : مضرب مشترک 18 و 12
2- عددهای 18 و 12 به صورت تجزیه شده، نوشته شده¬اند.
= [12 و 18] 12=2×2×3 18=2×3×3
با توجه به پاسخ بالا چه رابطه¬ای بین شمارنده¬های اول دو عدد و ک.م.م آنها می بینید؟ توضیح دهید. می-توانید از مثال زیر هم استفاده کنید.
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
کار در کلاس
1- تساوی 6×4=24 را به صورت¬های مختلف می¬توان معنا کرد؛ جاهای خالی را کامل کنید.
4 شمارندۀ ـــــــ است. ششمین مضرب ـــــــ عدد 24 است.
6 شمارندۀ ـــــــ است. چهارمین مضرب ــــــ عدد ـــــــ است.
عددهای ____ و ____ شمارنده¬های ____ هستند. عدد ____ بر ____ و ____ قابل قسمت است.
2 یکی از مهم ترین کاربردهای ک.م.م در پیدا کردن مخرج مشترک دو کسر است، یعنی کوچک ترین عددی را پیدا می¬کنیم که به هر دو مخرج بخش پذیر (قابل قسمت) باشد. مانند نمونه حاصل جمع ها و تفریق¬ها را با کمک ک.م.م مخرج ها به دست آورید.
تمرین
1- هر 20 دقیقه یک اتوبوس خط A از پایانۀ مسافربری حرکت می¬کند. اتوبوس¬های خط B هر 30 دقیقه از پایانه حرکت می¬کنند. ساعت 12 دو اتوبوس در خط¬های A و B همزمان حرکت کرده¬اند. در چه ساعتی به¬طور همزمان اتوبوس¬ها از این دو خط حرکت می¬کنند؟
2- یک پیست دوومیدانی کوچک در یک مجتمع فرهنگی ورزشی قرار دارد. امید و فرامرز از یک نقطه شروع به دویدن می کنند. اگر امید هر 35 ثانیه یک دور کامل میدان دو را طی کند و فرامرز هر 21 ثانیه یک دور کامل طی کند، پس از چند ثانیه فرامرز و امید با هم به همان نقطه شروع می رسند؟ در این صورت هر کدام چند دور دویده¬اند؟
3- آیا 210 مضرب مشترک 7 و 30 است؟ چرا؟
آیا 420 مضرب مشترک 7 و 30 است؟ چرا؟
دو عدد 7 و 30 چند مضرب مشترک دارند؟
4- دلیل درستی جملات زیر را بیان کنید.
* اگر عددی بر عدد دیگر بخش پذیر باشد، عدد بزرگ تر ک.م.م دو عدد است.
* اگر ب.م.م دو عدد یک باشد، ک.م.م دو عدد برابر حاصل ضرب دو عدد است.
* ک.م.م دو عدد اول برابر حاصل ضرب آن¬هاست.
5- برای هر کدام از جملات درستِ زیر یک مثال بزنید.
* [n و 1]=n
* [n و n]=n
* ب.م.م دو عدد شمارنده ک.م.م دو عدد است.
* حاصل ضرب دو عدد برابر حاصل ضرب ک.م.م و ب.م.م دو عدد است.
6- به صورت ذهنی تساوی¬ها را کامل کنید.
مرور فصل 5
مفاهیم و مهارت¬ها
در این فصل واژه های زیر به کار رفته¬اند. مطمئن شوید که می¬توانید با جملات خود آنها را تعریف کنید و برای هر کدام یک مثال بزنید.
* عدد اول * شمارندۀ (مقسوم¬علیه) یک عدد * شمارندۀ اول * مضرب * ب.م.م * ک.م.م
نوشتن شمارنده های یک عدد
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
پیدا کردن عددهای اول
پیدا کردن شمارنده اول یک عدد
ساختن عددهای مختلف با شمارنده های اول
پیدا کردن تمام شمارنده¬های یک عدد با معلوم بودن تجزیه عدد
تجزیه عدد به شمارنده¬های اول
پیدا کردن ب.م.م دو عدد
نوشتن مضرب¬های یک عدد
پیدا کردن ک.م.م دو عدد
رابطه بین مضرب و شمارنده
کاربرد
از مفاهیم ب.م.م و ک.م.م در محاسبات کسری (ساده کردن و مخرج مشترک) استفاده می کنیم. درک شمارنده¬های اول یک عدد زمینه ساز همین بحث به صورت جبری است.
تمرین¬های ترکیبی
در صورتی که تمرین های ترکیبی زیر را بتوانید انجام دهید، مطمئن می شوید که این فصل را به خوبی آموخته اید.
1- با توجه به تساوی 3×4=12 معانی مختلف آن را بیان کنید.
2- ابتدا دو عدد زیر را به شمارنده های اول تجزیه کنید، سپس ب.م.م وک.م.م آنها را به دست آورید.
= 60 = 70
3- عددهای اول بین 50 تا 80 را بنویسید.
4- با شمارنده های اول 2 و 3 دو عدد بنویسید که ب.م.م آنها 6 و ک.م.م آن¬ها 36 باشد.
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
فصل 6
سطح و حجم
اهمّیت بسته بندی محصولات غذایی کمتر از اهمّیت تولید آن محصول نیست. برای مثال در بسته بندی شیرینی و شکلات کیفیت و ظاهر بسته بندی در فروش آن تأثیر زیادی دارد. یکی از موضوعات مهم در این بسته بندی¬ها رابطه بین سطح و حجمی است که با آن سطح ساخته می شود.
حجم های هندسی
محاسبۀ حجم¬های منشوری
مساحت جانبی و کل
حجم و سطح
حجم¬های هندسی
فعالیت
1- به اطراف خود (کلاس، خانه، خیابان و…) به دقت نگاه کنید.
آیا چیزی پیدا می¬کنید که حجم نداشته باشد؟
در تصویر مقابل چه نوع حجم¬هایی را می بینید؟
آیا همه آن¬ها شکل هندسی دارند؟
آیا می¬توانید یک طبقه بندی از انواع حجم¬ها ارائه کنید؟
حجم¬ها را می¬توان به دو دستۀ هندسی و غیرهندسی تقسیم کرد. حجم¬های هندسی شکل¬های مشخص و تعریف شده دارند.حجم های هندسی را می توان به سه دسته اصلی تقسیم کرد. منشوری – کروی – هرمی. برخی از حجم¬های هندسی نیز ترکیبی از این سه نوع¬اند.
فعالیت
1- در تصویر فعالیت بالا حجم¬های هندسی را با و غیرهدسی را با × مشخص کنید.
در حجم¬های هندسی نوع آن را تعیین کنید.
در حجم¬های ترکیبی نیز مشخص کنید که از چه نوع حجم¬هایی ساخته شده¬اند.
2- با توجه به شکل¬های زیر خصوصیت های سه نوع حجم هندسی زیر را بنویسید.
حجم¬های منشوری: ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
حجم¬های هرمی: ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
حجم¬های کروی: ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
حجم¬های منشوری بین دو صفحه موازی قرار می¬گیرند.
به این دو سطح موازی که سطح منشوری را قطع می کنند، قاعده و به سطح¬های اطراف آن وجه¬های جانبی می گویند. به محل برخورد سطح¬ها یال و به نقطۀ برخورد هر سه سطح رأس می¬گویند.
کار در کلاس
1- در هر یک از منشورهای زیر مشخص کنید چند وجه جانبی دارد؛ یال¬ها، رأس¬ها و قاعده¬ها را نام ببرید.
تعداد وجه¬های جانبی:
رأس¬ها:
یال¬ها:
قاعده¬ها:
رأس¬ها:
یال¬ها:
قاعده¬ها:
تعداد وجه¬های جانبی:
رأس¬ها:
یال¬ها:
قاعده¬ها:
تعداد وجه¬های جانبی:
رأس¬ها:
یال¬ها:
قاعده¬ها:
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
2- برای اینکه در نام بردن یال و رأس چیزی جا نیفتد، از چه راهبردی استفاده می کنید؟
3- آیا استوانه هم یک حجم منشوری است؟ چرا؟
فعالیت
با خمیر مجسمه سازی (یا می توانید از یک سیب زمینی استفاده کنید) یک استوانه بسازید. با یک قیچی یا چاقو مانند شکل های مقابل آن را برش بزنید. سطح برش خورده را رنگ کنید و روی یک کاغذ بزنید، اثر آن به چه شکلی است؟
همین فعالیت را می¬توانید با برش های دیگر تکرار کنید. همچنین به جای استوانه می¬توانید منشورهای دیگری را هم امتحان کنید. به این کار مقطع زدن می¬گویند. نرم¬افزارهای زیادی هستند که می¬توانند این فعالیت را شبیه¬سازی کنند. در صورت تمایل از آن¬ها استفاده کنید.
تمرین
1- آیا ممکن است مقطع یک کره و یک استوانه هم شکل باشند؟ در چه صورت؟
آیا ممکن است مقطع یک منشور و یک هرم هم شکل باشند؟
2- یک استوانه از دید بالا به چه شکلی دیده می شود؟
یک منشور 6 پهلو به چه شکلی دیده می شود؟
رأس های منشوری با قاعده ٦ ضلعی منتظم روی دایره قاعده استوانه است.این حجم از بالا به چه شکلی دیده می شود؟
3- مشخص کنید هر کدام از حجم های زیر، ترکیبی از کدام حجم ها هستند؟
4- حجم مقابل را از 4 جهت نگاه می کنیم این حجم از 4 طرف به چه شکلی دیده می شود؟
5- قاعده منشورهای زیر را رسم کنید (در واقع دید از بالا یا همان مقطع منشور است).
6- بلورهای (مصوب فرهنگستان Crystal) معدنی به طور طبیعی شکل می¬گیرند، ولی دارای حجم هندسی-اند. برای نمونه مشخص کنید 3 بلور زیر از چه حجم¬هایی درست شده¬اند؟
محاسبه حجم¬های منشوری
فعالیت
1 در دوره دبستان آموختید که حجم یک مکعب مستطیل برابر است با حاصل ضرب طول، عرض و ارتفاع. با توجه به درس جبر که در فصل قبل آموختید، حجم مکعب مستطیل را با یک رابطه جبری نشان دهید.
= V حجم
2- قاعدۀ مکعب مستطیل از 8 مربع به ضلع یک سانتی¬متر درست شده است. (4 × 2) اگر روی این قاعده، مکعب مستطیلی به ارتفاع 2 سانتی¬متر درست کنیم، حجم آن چقدر می¬شود؟
اگر قاعدۀ مکعب مستطیل 4×3 باشد، با همات ارتفاع چه حجمی درست می¬شود؟
3- همچنین آموختید که واحد حجم مکعبی به ضلع 1 سانتی متر یا 1 متر، یک سانتی متر مکعب یا یک مترمکعب می گویند. مشخص کنید که هر کدام از حجم های زیر از چند مکعب واحد درست شده¬اند.
4- اکنون هر کدام از شکل های زیر را به مربع هایی به ضلع 1 سانتی متر تقسیم کنید تا مشخص شود قاعده هر کدام چند مربع به
ضلع یک سانتی متر است (می توانید از عددهای کسری هم استفاده کنید).
اگر روی این قاعده ها منشوری به ارتفاع 3 سانتی متر درست کنیم، حجم هر کدام چقدر می شود؟ اگر به همین ترتیب بتوانیم مساحت قاعده هر منشور را با مربع های واحد سطح تقریب بزنیم، چگونه می توانیم حجم شکل های منشوری را به دست آوریم؟ برای مثال قاعده یک استوانه را که به شکل دایره است، با مربع های واحد تقریب بزنید و حجم استوانه به ارتفاع 3 سانتی متر را به طور تقریبی به دست آورید.
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
کار در کلاس
1- با توجه به فعالیت صفحۀ قبل، رابطۀ جبری به دست آوردن حجم¬های منشوری (V) را که در آن مساحت قاعدۀ منشور (S) و ارتفاع منشور (h) است، بنویسید.
2- با توجه به رابطه بالا و مساحت قاعده داده شده، حجم هر شکل را محاسبه کنید.
3- ابتدا مساحت قاعده و سپس حجم هر یک از اجسام زیر را حساب کنید. برای به دست آوردن مساحت و حجم هر شکل رابطه های جبری را بنویسید.
4- منبع آبی به شکل استوانه است که شعاع قاعدۀ آن 8/0 متر و ارتفاعش 2 متر است. این منبع چند متر مکعب آب می¬گیرد؟
5- یک جعبه دستمال کاغذی به شکل مکعب مستطیل داریم که طول آن 25 ، عرض آن 12 و ارتفاعش 5 سانتی متر است. تعیین کنید چند عدد از این جعبه ها در یک کارتن که به شکل مکعب مستطیل به ابعاد 50 و 30 و 24 سانتی متر است، جا می گیرد؟
تمرین
1- حجم ستون شکل مقابل را به صورت تقریبی پیدا کنید.
(کل شکل را مکعب مستطیل و یا استوانه درنظر بگیرید.)
حالا کمی دقیق تر محاسبه کنید و آن را به سه قسمت تقسیم کنید و حجم سه تکه را جداگانه حساب کنید
و مجموع را به دست آورید (شعاع قاعده استوانه چند است؟).
تفاوت دو جواب را به دست آورید.
2- حجم اشکال زیر را به دست آورید.
3- چاهی به عمق 1 متر حفر کرده¬ایم. شعاع دهانۀ این چاه 4/0 متر است. وقتی خاک کنده و بیرون ریخته می¬شود، حجم آن 3/1 برابر می¬شود. اگر خاک این چاه بعد از بیرون آمدن در سطحی به ابعاد 4 و 5 متر به طور یکنواخت ریخته شود تا یک مکعب مستطیل به وجود آید، ارتفاع این مکعب مستطیل چقدر خواهد شد؟
4- حوضی است به شکل مکعب مستطیل که ابعاد آن 4 و 3 و 5/1 متر است. این حوض خالی را با شیر آبی که در هر دقیقه 60 لیتر آب وارد آن می¬کند، پر می¬کنیم. چند ساعت طول می¬کشد تا حوض پر شود؟
5- یک پارچ به شکل استوانه است که ارتفاع آن 30 سانتی¬متر و شعاع قاعدۀ آن 8 سانتی¬متر است. آب داخل این پارچ را در لیوان¬هایی به شکل استوانه که ارتفاع آن¬ها 10 سانتی¬متر و شعاع قاعدۀ آن 4 سانتی¬متر است، می¬ریزیم. این آب چند لیوان را پُر می¬کند؟
6- قاعده یک منشور سه پهلو مثلث قائم الزاویه¬ای که اندازه ضلع های قائمه آن 3 و 4 است. ارتفاع این منشور 6 سانتی متر است. حجم این منشور را پیدا کنید.
مساحت جانبی و کل
فعالیت
1- مساحت همه وجه های جانبی منشورهای زیر را به دست آورید. هر وجه جانبی چه شکلی دارد؟ به مجموع این مساحت ها مساحت جانبی شکل می گویند.
5- برای به دست آوردن مجموع مساحت جانبی منشور سه پهلوی بالا به صورت زیر، آن را روی کاغذ قرار می¬دهیم، و به اندازه طول هر ضلع یک علامت می گذاریم.
با توجه به شکل¬های بالا چگونه می¬توانستیم ساده¬تر مساحت جانبی را به دست آوریم؟
3- با توجه به 2 سؤال بالا اگر مساحت را با S، محیط را یا P و ارتفاع را با h نشان دهیم. رابطۀ جبری مساحت منشورهای بالا را بنویسید.
کار در کلاس
1- مساحت جانبی شکل¬های زیر را پیدا کنید.
2- ستونی به شکل منشور 6 پهلوست که هر ضلع آن 2/0 متر و ارتفاع آن 5 متر است. می¬خواهند بدنۀ جانبی این ستون را کاشی¬کاری کنند. چند متر مربع کاشی لازم است؟
فعالیت
1- یک استوانه را به شکل زیر روی یک صفحه می¬غلتانیم و ابتدا و انتهای کار را مشخص می کنیم.
با این کار چه شکلی به دست می آید؟
طول و عرض آن چگونه به دست می آید؟
مساحت این شکل چگونه به دست می آید؟
2- با توجه به سؤال بالا مساحت جانبی یک استوانه به ارتفاع h و شعاع قاعدۀ r را با عبارت جبری نشان دهید.
کار در کلاس
1- با توجه به سؤال بالا با یک مستطیل می توان یک سطح استوانه ای درست کرد.
این سطح استوانه را روی کاغذ بگذارید و دور آن خط بکشید. این دایره، قاعده استوانه است. چون استوانه 2 قاعده دارد.
2- دایره و یک مستطیل مساحت کل استوانه را تشکیل می دهند.
شکل مقابل را گستردهٔ استوانه می گویند.
چه رابطه ای بین دایره و مستطیل در این گسترده وجود دارد؟
2- گسترده یک منشور 6 پهلو با قاعده 6 ضلعی منتظم و گسترده یک مکعب مستطیل با قاعده مربع در
شکل¬های زیر رسم شده اند.
چه رابطه ای بین قاعده ها و مستطیل ها وجود دارد؟
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
تمرین
1- در شکل زیر گستردۀ چند منشور داده شده است. آنها را روی کاغذ بکشید و منشورها را درست کنید و به کلاس بیاورید.
در چه صورت گسترده شکل وسط به یک مکعب تبدیل می شود؟
2- یک غلتک روی زمین آسفالت شده باید 4 بار غلت بزند تا سطح آن صاف شود. اگر شعاع غلتک 50 سانتی متر و ارتفاع استوانه آن 1 متر باشد، برای آسفالت کردن سطح یک کوچه به طول ٢٠ و عرض ٤ متر، این غلتک باید به طور تقریبی چند بار بچرخد؟
3- یک چرخ ماشین که کاملاً خیس شده است، با 10 دور چرخیدن روی زمین جای خود را مشخص می کند تا خشک شود. اگر این چرخ به ضخامت 20 سانتی متر و قطر 70 سانتی متر باشد، چه مساحتی از زمین را خیس خواهد کرد؟
4- یک چادر مسافرتی به شکل مقابل است.چند متر پارچه برای ساخت آن به کار رفته است؟ حجم این چادر چقدر است؟
5- یک مخزن نفت به شکل استوانه ای است که شعاع قاعده آن 3 متر و ارتفاعش 5 متر است. می¬خواهیم بدنه خارجی و سقف آن را رنگ بزنیم. اگر هزینه رنگ کردن هر متر مربع 3000 تومان باشد، برای رنگ کردن این مخزن چقدر باید هزینه کرد؟
6- می¬خواهیم با مقوا مکعبی به ضلع 10cm بسازیم. چند سانتی¬متر مربع مقوا به کار می¬رود؟
7- یک جعبه به شکل مکعب مستطیل به ابعاد 30 و 50 و 40 سانتی متر را با کاغذ کادو پوشانده ایم. برای پوشاندن این جعبه حداقل چند سانتی مترمربع کاغذ کادو لازم داریم؟ چرا در این مسئله حداقل کاغذ لازم خواسته شده است؟
8- با مکعب های به ضلع 1 واحد حجم مقابل را ساخته ایم. اگر تمام سطح های این حجم را رنگ کنیم، چند مکعب رنگ نمی شوند؟
چند مکعب رنگ می شود؟
چند مکعب 2 وجهشان رنگ می شود؟
چند مکعب 3 وجهشان رنگ شده است؟
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
حجم و سطح
فعالیت
1- یک مستطیل به طول و عرض داده شده را به دو صورت زیر لوله می کنیم تا استوانه به دست آید.
در هر حالت حجم استوانه را به دست آورید. مانند نمونه از رابطه¬های جبری کمک بگیرید. برای ساده¬تر شدن محاسبه¬ها عدد پی (π) را در 3 در نظر بگیرید. در هر حالت ابتدا شعاع قاعده و ارتفاع استوانه را تشخیص دهید.
با مقایسهٔ حجم ها و با توجه به اینکه هر دو حجم با یک مستطیل ساخته شده است، چه نتیجه ای می گیرید؟
2- یک کارخانۀ تولید چای دو نوع بسته¬بندی به شکل¬های زیر ارائه می¬کند. هر دو نوع قوطی با ورق روی-اندود (مصوب فرهنگستان galvanized) درست شده¬اند. در کدام یک چای بیشتری جا می¬گیرد.
در کدام یک ورق روی¬اندود بیشتری برای ساخت قوطی به کار رفته است؟ در محاسبات خود عدد π را 3 در نظر بگیرید.
باتوجه به عددهای بالا اگر شما مدیر کارخانه باشید، کدام نوع بسته بندی را انتخاب می کنید؟ چرا؟
کدام نوع بسته بندی در حمل و نقل بهتر است و جای کمتری می گیرد؟ چرا؟
کار در کلاس
برای بسته بندی شیرینی، جعبه هایی را درست می کنند. شکل گسترده این جعبه ها به صورت زیر است و پس از تا کردن مربع های کوچک گوشه ها روی هم قرار می گیرند و جعبه درست می شود.
با توجه به اندازه های داده شده، حجم (گنجایش) جعبه را پیدا کنید.
اگر به جای 5 سانتی متر لبه ها را 6 سانتی متر درنظر بگیریم، جعبه ای که با همین مقوا ساخته می شود، حجم بیشتری دارد یا کمتر؟
فعالیت
مستطیل ABCD را حول محوری که از AD می¬گذرد، دوران می¬دهیم. شکل زیر نشان می¬دهد که مستطیل¬ها چگونه حرکت می¬کنند.
شما هم مانند شکل مقابل کاغذی را روی مدادی بچسبانید و آن را بچرخانید و حرکت مستطیل را تماشا کنید.
با چرخاندن این مستطیل چه حجمی به وجود می آید؟ مشخصات آن حجم را بنویسید.
با حرکت یک سطح در فضا، حجم ساخته می شود. همین کار را برای شکل های دیگر نیز می توان انجام داد تا حجم های دیگری ساخته شوند. در سال های بعد در این مورد بیشتر توضیح داده خواهد شد.
کار در کلاس
1- سطحی مثل شکل مقابل را حول محور D دوران می¬دهیم.
حجم چه شکلی ساخته می شود؟ می توانید با یک فرفره و چرخاندن آن حجم ایجاد شده را ببینید. از این خاصیت در خرّاطی، تراشکاری و سفالگری برای ساختن حجم های مختلف استفاده می کنند.
2- یک مستطیل را یک بار حول محور AD و یک بار حول محور AD دوران دهید. حجم حاصل از این دوران را حساب کنید.
تمرین
1- یک مقوا به طول و عرض، 5×20 را به شکل استوانه به ارتفاع 5 در آورده¬ایم. یک مقوای دیگر را نیز به ابعاد 10×10 را به شکل یک استوانه در آورده¬ایم. با توجه به اینکه مساحت مقواها در دو حالت برابر است، کدام استوانه حجم بیشتری دارد؟
2- با شکل مقابل یک منشور درست کرده ایم. مساحت جانبی آن را پیدا کنید.
3- یک صابون مکعب مستطیل شکل به حجم 32 سانتی¬متر مکعب پس از چند بار مصرف، کوچک شده و به ابعاد 2 1/2 و 4 و 1 1/2 سانتی¬متر تبدیل شده است. چند درصد این صابون استفاده شده است؟
4- یک استوانه که با یک مقوا به طول 20 سانتی متر و عرض 10 سانتی متر ساخته شده به طور تقریبی چه حجمی دارد؟ (ارتفاع استوانه 20 است.)
5- اگر یک حجم از بالا و سمت راست و روبه رو به صورت زیر دیده شود، آن حجم را رسم کنید.
6- شکل مقابل گسترده یک منشور را نشان می دهد. مساحت جانبی منشور را پیدا کنید.
7- با توجه به حجم منشور و ابعاد آن، اندازهٔ ضلع های گستردهٔ آن را بنویسید.
8- حجم مقابل از راست، بالا و روبه رو چگونه دیده می شود؟
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
مرور فصل 6
مفاهیم و مهارت¬ها
در این فصل واژه های زیر به کار رفته اند. مطمئن شوید که می توانید با جملات خود آنها را تعریف کنید.برای هر کدام مثال بزنید.
* حجم هندسی * حجم منشوری * مساحت جانبی * مساحت کل *گسترده
در این فصل روش های اصلی زیر مطرح شده اند.با یک مثال هر کدام را توضیح دهید و در دفتر خود یک خلاصه تهیه کنید.
انواع حجم های هندسی
حجم مخروطی و حجم منشوری
قاعده، وجه، یال و رأس حجم های منشوری
مقطع زدن یک حجم منشوری
رابطه پیدا کردن حجم های منشوری
رابطه پیدا کردن مساحت جانبی حجم های هندسی
رابطه پیدا کردن مساحت کل حجم های منشوری
ساختن یک حجم به کمک گسترده آن
دوران سطح حول یک محور و ساختن حجم
مقایسه حجم هایی که با یک سطح مشخص درست شده اند.
کاربرد
کاربرد این فصل در زندگی روزمره فراوان است. در دنیایی از اجسام زندگی می کنیم و نیاز داریم حجم های مختلف را اندازه بگیریم و برای ساختن حجم ها نیز از سطح ها )کاغذ، مقوا،ورق و …( استفاده می کنیم.
تمرین¬های ترکیبی
در صورتی که تمرین های ترکیبی زیر را توانستید انجام دهید، مطمئن می شوید که این فصل را به خوبی آموخته اید.
1- حجم، مساحت جانبی و مساحت کل شکل های زیر را به دست آورید.
استوانه به شعاع قاعده 2 و ارتفاع 2 منشور چهار پهلو با قاعده مربع به ضلع 2 و ارتفاع 20
2- الف) با توجه به شکل مکعب مستطیل اندازه ضلع های خواسته شده روی گسترده آن را مشخص کنید.
ب) حجم شکل مقابل را به دست آورید.
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
فصل 7
توان و جذر
وقتی یک یاخته (مصوب فرهنگستان Cell, cellule) به یاخته¬های دیگر تبدیل می¬شود و این عمل تکرار می¬گردد، در مدت کوتاهی تعداد یاخته¬ها به سرعت افزایش پیدا می¬کنند.
رشد تعداد یاخته ها به صورت توانی است. شاید به همین علت است که جراحت پوست در مدت کوتاهی ترمیم می شود و یاخته های جدید جایگزین یاخته های مرده می شوند.
تعریف توان
محاسبۀ عبارت های توان دار
ساده کردن عبارت های توان دار
جذر و ریشه
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار
تعریف توان
فعالیت
1- امید می داند که نوه چهار نفر است. این چهار نفر پدربزرگ ها و مادربزرگ های امیدند. او می خواهد بداند که نتیجه چند نفر است؟ (به فرزند نوه، نتیجه می گویند). امید برای پاسخ سؤال خود شکل مقابل را کشید.
الف) شکل را کامل کنید و با استفاده از آن بگویید که امید نتیجه چند نفر است؟
ب) به نظر شما تعداد افرادی که امید نبیره آنها است، چند نفرند؟ (به فرزند نتیجه، نبیره می گویند.)
ج) جدول مقابل را کامل کنید. برای محاسبه تعداد، از ماشین حساب نیز می توانید کمک بگیرید.
2- یک کاغذ را چند بار تا می زنیم و هر بار تعداد قسمت هایی را که کاغذ تقسیم شده است، می شماریم. چه الگویی در تعداد قسمت ها می بینید؟
اگر تا زدن را به همین ترتیب ادامه دهیم، در تای هشتم چند قسمت خواهیم داشت؟
در تای دهم چند قسمت خواهیم داشت؟
در تای nام چند قسمت خواهیم داشت؟
چه راهی برای خلاصه کردن عبارت های بالا پیشنهاد می کنید؟
(با توجه به اینکه در عمل، تا کردن کاغذ تا چندمرحله بیشتر ممکن نخواهد بود، برای یافتن جواب ها از شکل های داده شده استفاده کنید.)
عبارتی مانند 2×2×2×2×2 را در ریاضیات برای ساده¬تر شدن به صورت 2^5 می¬نویسیم و آن را چنین می¬خوانیم: 2 به توان 5. در عبارت 2^5، 2 را پایه و 5 را توان می¬نامیم. درست شبیه همان کاری که در ساده کردن و خلاصه کردن جمع انجام می¬دادیم.
(2+2+2+2+2=5×2)
کار در کلاس
1- جدول مقابل را کامل کنید. پس از آن عبارت های زیر را به صورت ساده شده بنویسید.
2- عددهای داده شده را مانند نمونه تجزیه کنید و به صورت عدد توان دار بنویسید.
3- کدام یک درست وکدام یک نادرست است؟ در صورت امکان موارد نادرست را اصلاح کنید.
4- تساوی ها راکامل کنید.
5- درتکثیر یاخته ها، هر یاخته به 2 یاخته تقسیم می شود. دوباره هرکدام از آن یاخته ها خودشان به 2 یاخته تقسیم می شوند و این کار ادامه پیدا می کند. جدول زیر را کامل کنید و حاصل را به صورت عدد توان دار بنویسید.
تمرین
1- با توجه به شکل های زیر مساحت و حجم های خواسته شده را با عبارت های توان دار جبری نمایش دهید.
2- جمله های کلامی زیر را به صورت عبارت جبری نشان دهید.
هر عدد به توان یک برابر خودش می شود: a^1=a
یک به توان هر عدد برابر یک می شود:
مجذور هر عدد؛ یعنی آن عدد به توان 2: = مجذور a
مکعب یک عدد؛ یعنی آن عدد به توان 3: = مکعب x
صفر به توان هر عدد به جز صفر برابراست با:
3- تعداد مکعب¬های کوچک 1×1×1 را در هر شکل با یک عدد توان¬دار نشان دهید.
4- حاصل هر عبارت توان دار را به دست آورید.
5- مقدار عبارت 3^n را به ازای عددهای داده شده به دست آورید.
6- حاصل عددهای را به دست آورید و به صورت نمودار ستونی در دفتر خود رسم کنید (باید واحد مناسبی برای محور عمودی رسم کنید). در مورد شیوۀ رسم هر ستون توضیح دهید، آیا می¬توانید 2^6 یا 2^7 را در دفتر خود رسم کنید؟ چرا؟
7- عدد 〖11〗^12 به طور تقریبی چند رقمی است؟ چرا؟
فعالیت
محاسبّ عبارت توان¬دار
فعالیت
ترتیب انجام عملیات را در دوره دبستان آموخته اید. با توجه به درس توان، ترتیب انجام دادن عملیات مختلف ریاضی به صورت
1) پرانتز 2) توان 3) ضرب و تقسیم 4) جمع و تفریق انجام می شود.
با کامل کردن مراحل محاسبه عبارت و همچنین ترتیب انجام عملیات و نحوه نوشتن راه حل توجه کنید.
محاسبه های بعدی را کامل کنید.
کار در کلاس
1- حاصل عبارت ها را به دست آورید.
2- کدام یک درست و کدام یک نادرست است؟ دلیل خود را توضیح دهید.
3- روش محاسبه را توضیح دهید.
فعالیت
1- مانند نمونه عبارت های توان دار را حساب کنید.
با توجه به توان ها و حاصل عبارت ها چه نتیجه ای می گیرید؟
2 عبارت های زیر را حساب کنید.
3- الگوی عددی زیر را کامل کنید.
ارتباط بین عددهای توان دار و حاصل آنها را توضیح دهید.
به نظر شما در جای خالی چه عددی باید نوشت؟
کار در کلاس
1- حاصل عبارت های زیر را به دست آورید.
2- در جای خالی علامت < یا = یا > بگذارید.
تمرین
1- کدام درست و کدام نادرست اند؟ علت نادرستی را توضیح دهید.
2- الف) حاصل عبارت های زیر را به دست آورید.
ب) با توجه به تمرین های بالا عددهای زیر را به صورت گسترده و سپس به صورت توانی نمایش دهید.
3- به جای n عددهای 1 تا 5 را قرار دهید دو عبارت 4^n و n^4 را با هم مقایسه کنید. برای محاسبات از ماشین حساب استفاده کنید.
برای n=10 کدام یک بزرگ¬تر از دیگری است؟
4- در بعضی از ماشین حساب ها کلید توان به صورت زیر استفاده می شود. عددهای توان دار را محاسبه می کنند. برای مثال 2^3 به صورت زیر محاسبه می شود. حالا شما عددهای مختلف را در ماشین حساب وارد و حاصل آنها را ملاحظه کنید. چه راه دیگری برای پیدا کردن جواب 2^3 وجود دارد؟
5- حاصل عبارت ها را به ازای عددهای داده شده به دست آورید.
ساده کردن عبارت¬های توان¬دار
فعالیت
1 زهره می خواست مسئله هایی را که معلم برای تمرین تعیین کرده بود، حل کند. معلم ریاضی خواسته بود که دانش آموزان مساحت مستطیل به طول 2^4 و عرض 2^3را به دست آورند. زهره به صورت زیر عمل کرد و عبارت ها را به صورت ضرب نوشت.
سیما با مشاهده عبارت زهره به او گفت: هفت تا ٢ ضرب شده است. پس عبارت تو با 2^7 برابر است. نتیجه گیری سیما را با یک تساوی نشان دهید.
2- مانند نمونه عمل کنید.
با توجه به تساوی های بالا یک رابطه برای ساده کردن ضرب عبارت های توان دار با پایه های مساوی بنویسید.
3 با توجه به رابطه بالا، مانند نمونه عبارت توان دار را به صورت ضرب 2 یا چند عبارت توان دار بنویسید.
کار در کلاس
1- حاصل عبارت های زیر را به صورت یک عدد توان دار بنویسید.
2- با باز کردن عبارت توان دار، جواب را ساده تر کنید و محاسبات را مانند نمونه پاسخ دهید.
3- اگر 2^10=1024 باشد حاصل 2^12 را به دست آورید.
فعالیت
1- مانند نمونه عبارت ها را باز کنید و دوباره به صورت عدد توان دار بنویسید.
با مقایسه تساوی ها یک قانون کلامی برای ساده کردن ضرب عبارت های توان دار با توان¬های مساوی به دست آورید.
2- با قانونی که به دست آوردید، عبارت های زیر را ساده کنید.
3- به تساوی های روبه رو توجه کنید.
مانند نمونه های بالا عددهای توان دار زیر را باز کنید.
کار در کلاس
1- مانند نمونه عبارت های توان دار را تا جایی که ممکن است ساده کنید.
2- عبارت توان¬دار مقابل را تا جایی که ممکن است، ساده کنید. 2^a×2^b=
به جای a و b عددهای 3 و 5 یک بار 4 و 7 قرار دهید و تساوی¬ها را به صورت عددی بنویسید.
تمرین
1- در تساوی زیر به جای a و b و c عددهای مختلفی قرار دهید و تساوی¬های عددی بسازید.
2) با استفاده از تجزیه به عددهای اول، هر عدد را به صورت توان دار بنویسید.
3) مسئله هایی طرح کنید که پاسخ آنها: الف) 2^3 ب) 3×2 ج) 5^2 باشد.
4)عددهای توان دار را از کوچک به بزرگ مرتب کنید.
5) کدام یک درست و کدام یک نادرست است؟ توضیح دهید.
6- کدام یک از عبارت¬های زیر 〖(2/3)〗^3 را نشان می¬دهید؟
7- به جدول زیر توجه کنید و با توجه به آن سؤال ها را جواب دهید.
حاصل عبارت 65536×4096 را به صورت توان¬دار بنویسید.
تعداد رقم¬های 4^10 را پیش¬بینی کنید. فکر می¬کنید. 4^20 چند رقمی می¬شود؟ چرا؟
8- جاهای خالی را کامل کنید. چه الگویی مشاهده می کنید؟ یک تساوی دیگر بنویسید.
آیا این الگو برای 3^3-1^3=2^4 درست است؟
9- در جای خالی یکی از عمل¬های + یا – یا × یا ÷ را قرار دهید تا تساوی برقرار باشد.
جذر و ریشه
فعالیت
1- مساحت یک زمین بازی کودکان که به شکل مربع است، برابر 144 متر مربع است. طول ضلع این مربع چند متر است؟
2- یک شرکت برای محوطه¬سازی، سنگ¬های مرمر در اندازه¬های 50×25 سانتی¬متر خریده است. این شرکت در مجموع 81 متر مربع سنگ برای این کار خریده است. ضلع بزرگ¬ترین مربعی که می¬توان با این سنگ¬ها ساخت چند متر است؟
3- در جدول زیر طول ضلع تعدادی مربع و مساحت آنها داده شده است. جاهای خالی را کامل کنید.
4- در الگوی عددی زیر آیا عدد ١٥ قرار می گیرد؟ چرا؟
با کمک ماشین حساب و راهبرد حدس و آزمایش، عددی پیدا کنید که بتوان به جای x قرار داد.
در تساوی 3^2=9 هدد 9 را توان دوم یا مجذور عدد 3 و عدد 3 را نیز ریشۀ دوم یا جذر 9 می¬نامند. آیا 3- نیز ریشۀ دوم 9 است؟ چرا؟
جدول زیر را کامل کنید.
دانلود رایگان اپلیکیشن ریاضی هفتم از کافه بازار